ОПРЕДЕЛИТЕЛИ
2.1. Определители второго порядка
Пусть дана квадратная матрица второго порядка:
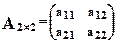 .
.
Определителем второго порядка будем называть число(D),полученное из квадратной матрицы второго порядка по формуле:
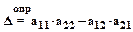 .
.
Другие обозначения определителя:
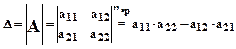 .
.
2.2. Определители третьего порядка
Пусть дана квадратная матрица третьего порядка: 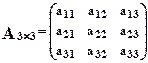 .
.
Определителем третьего порядка (D),будем называть число, полученное из квадратной матрицы третьего порядка по формуле: 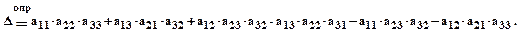
Другие обозначения: 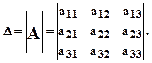
Минором элемента aij (Mij)будем называть определитель, полученный из данного после вычеркивания i-ой строки и
j-го столбца.
Пример: 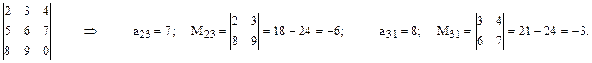

Из определения минора следует:
- минор это тоже определитель, только его порядок на единицу меньше, чем у данного;
- минор определителя второго порядка это элемент данного определителя, его называют также определителем первого порядка.
Алгебраическим дополнением элемента aij (Aij) будем называть минор этого элемента, умноженный на (-1)i+j. 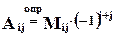 .
.
Свойства:
2.2.1. Транспонирование матрицы не меняет величину ее определителя.
Следствие: все свойства, справедливые для строк определителя, будут справедливы также и для его столбцов.
2.2.2. Если две строки поменять местами, то абсолютная величина определителя не изменится,
Дата добавления: 2015-08-26; просмотров: 696;
