Определители: вычисление и свойства
Цель: Изучить основные понятия темя, методы вычисления определителя, знать и уметь применять его свойства.
Всякую квадратную матрицу можно охарактеризовать числом, которое называется определитель или детерминант и может обозначаться одним из следующих символов: 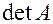 ,
,  ,
, 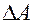 ,
, 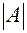 ,
, 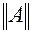
Прежде чем вычислять определитель введем в рассмотрение следующие определения.
Определение. Минором 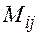 произвольного элемента
произвольного элемента  матрицы
матрицы 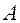 размерности
размерности 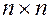 называется определитель порядка
называется определитель порядка 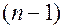 , полученный из основного определителя матрицы путем вычеркивания
, полученный из основного определителя матрицы путем вычеркивания 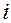 - ой строки и
- ой строки и 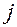 -го столбца.
-го столбца.
Пример: Для матрицы 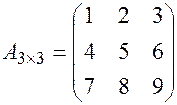 найти миноры
найти миноры 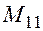 ,
,  .
.
Для вычисления минора 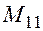 вычеркиваем из определителя первую строку и первый столбец. Все, что осталось от определителя есть искомый минор:
вычеркиваем из определителя первую строку и первый столбец. Все, что осталось от определителя есть искомый минор: 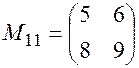 .
.
Для вычисления минора  вычеркиваем из основного определителя строку с номером два и столбец с номером три:
вычеркиваем из основного определителя строку с номером два и столбец с номером три: 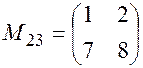 .
.
Определение: Алгебраическим дополнением 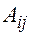 элемента
элемента 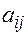 матрицы
матрицы 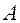 размерности
размерности 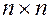 называется выражение вида:
называется выражение вида:
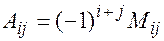 (11.1)
(11.1)
Другими словами, алгебраическое дополнение есть минор, взятый со своим знаком. Знаки алгебраического дополнения для матрицы третьего порядка можно записать в виде таблицы 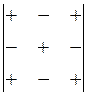 .
.
Теорема (о разложении определителя). Каков бы ни был номер столбца 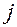 , для определителя порядка
, для определителя порядка  справедлива формула:
справедлива формула:
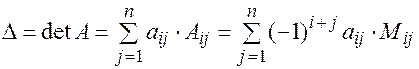 (11.2)
(11.2)
Разложения по строке , где 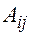 -алгебраическое дополнение элемента
-алгебраическое дополнение элемента 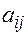 ,
, 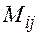 - минор элемента
- минор элемента  матрицы
матрицы 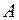 .
.
Каков бы ни был номер строки 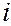 , для определителя порядка
, для определителя порядка  справедлива формула:
справедлива формула:
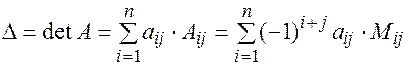 (11.3)
(11.3)
Разложение по столбцу.
Методы вычисления определителя:
При 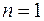 определитель равен самому элементу, т.е.
определитель равен самому элементу, т.е. 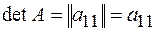 .
.
При 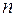 =2:
=2: 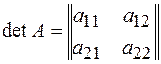 =
= 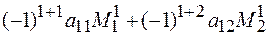 =
=
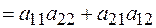 .
.
Дата добавления: 2015-08-26; просмотров: 644;
