Линейные комбинации строк и столбцов. Базисные строки и столбцы. Линейная независимость. Ранг матрицы. Вычисление ранга.

Цель: изучить понятие линейной комбинации и линейной независимости строк и столбцов матрицы, методы вычисления ранга и определения базисного минора.

В теме «матрицы и действия над ними» мы ввели понятия матрицы строки и матрицы столбца,

Определение. Столбец 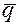назовем линейной комбинацией столбцов 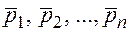одинаковой высоты, если при некоторых числах 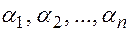имеет место равенство:

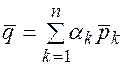(12.1)

Или в развернутом виде:

.

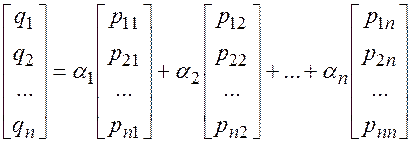В силу определения умножения матриц на число и операции сложения последнее равенство можно представить в виде системы равенств, составленных для каждого элемента:

;

;

…

.

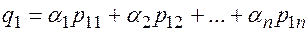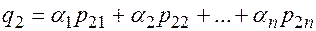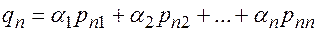По аналогии с линейной комбинацией введем понятие линейной независимости строк и столбцов матрицы. Пусть 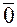- столбец у которого все элементы равны нулю.

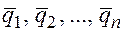Определение. Система из столбцов называется линейно независимой, если из равенства 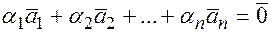следует, 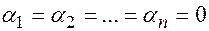. В противном случае, если не все 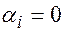( ), система столбцов линейно зависима.

Все утверждения записанные для столбцов, справедливы и для строк матрицы.

Пример: Столбцы

, ,

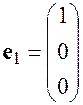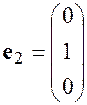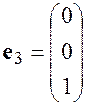
линейно независимы, т.к. их линейная комбинация

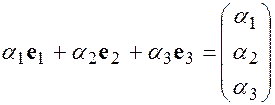
равна нулевому столбцу, только в случае, когда 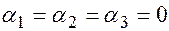, т.е. является тривиальной.