Матрицы и действия над ними
Цель: Изучить понятие матрицы, виды матриц, основные понятия, действия над матрицами и их свойства.
Определение: Система действительных или комплексных чисел (или функций) записанная в виде прямоугольной таблицы называется матрицей содержащая некоторое количество 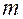 строк и
строк и  столбцов. Числа
столбцов. Числа 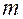 и
и  называются порядком матрицы.
называются порядком матрицы.
Матрицу записывают в виде:
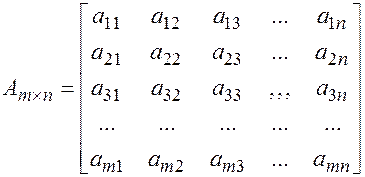 или
или
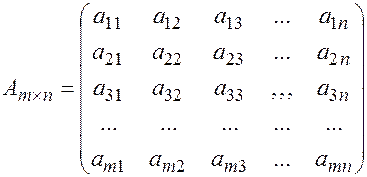
Числа 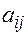 - называются элементами матрицы. Индексы
- называются элементами матрицы. Индексы 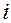 и
и 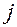 - указывают на место элемента в матрице:
- указывают на место элемента в матрице: 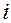 - номер строки,
- номер строки, 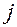 - номер столбца. (
- номер столбца. ( 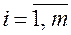 ,
, 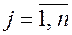 ).
).
Для краткости матрицы иногда записывают в виде: 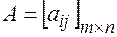 ,
, 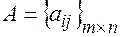 ,
, 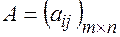 .
.
Определение: Матрица, у которой число строк равно числу столбцов называется квадратной. Для нее вводится понятие главной и побочной диагоналей. Главная диагональ идет из левого верхнего угла в правый нижний угол. Побочная – из верхнего правого угла в левый нижний.
Виды матриц:
1. Треугольные матрицы: все элементы лежащие выше или ниже главной (побочной) диагонали равны нулю.
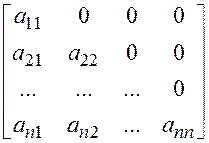
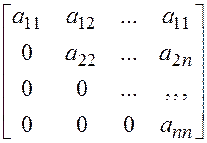
Нижняя треугольная верхняя треугольная
2. Диагональные матрицы: ненулевые элементы стоят только на главной диагонали. Т.е. 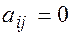 для всех
для всех 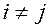
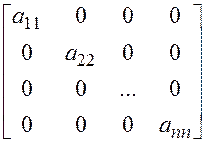
Особое место среди диагональных матриц занимает единичная матрица:
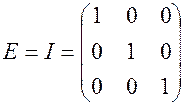 , ее элементы
, ее элементы 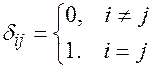
3. Симметричные матрицы: все ее элементы симметричны относительно главной диагонали.
4. Матрица, все элементы которой равны нулю называется нуль-матрицей и обозначается 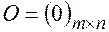
Матрица размерности 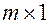 называется матрицей столбцом, просто столбцом или вектор столбцом.
называется матрицей столбцом, просто столбцом или вектор столбцом.
Матрица размерности 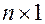 называется матрицей строкой, просто строкой или вектор строкой.
называется матрицей строкой, просто строкой или вектор строкой.
Матрица столбец - 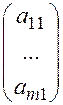 , матрица строка -
, матрица строка - 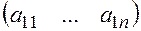 .
.
Определение: матрицы называются равными, если они имеют одинаковые порядки и их соответствующие элементы равны: 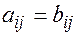 , для любых
, для любых 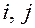 .
.
Операции над матрицами:
Определение. Суммой двух матриц 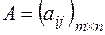 и
и 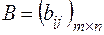 одинаковой размерности называется матрица
одинаковой размерности называется матрица 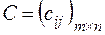 той же размерности, каждый элемент которой равен
той же размерности, каждый элемент которой равен
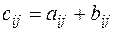 (10.1)
(10.1)
( 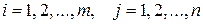 ),
), 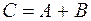 (матричная запись суммы двух матриц).
(матричная запись суммы двух матриц).
Из определения суммы матриц видим, что строки можно рассматривать как координаты векторов и соответственно производить операции над матрицами, как над векторами.
Дата добавления: 2015-08-26; просмотров: 985;
