Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости

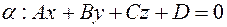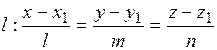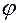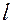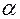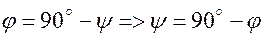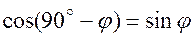Пусть даны плоскость , и прямая (рис 9.5) – угол между прямой и плоскостью . Определим его значение. Т. к. , и . Мы получили, что угол между прямой и плоскостью можно вычислить по формуле:

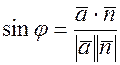(9.5)

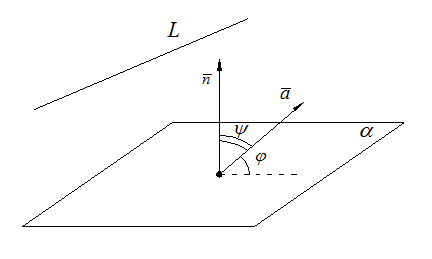
Рис. 9.5

Подставляя координаты векторов получим выражение .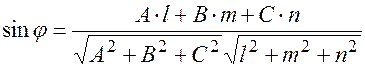

Если прямая параллельна плоскости, 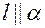, то 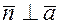и следовательно 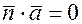или .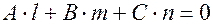

Если прямая ортогональна плоскости 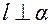, то 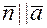и выполняется пропорция .

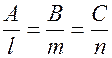Для того чтобы прямая 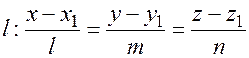принадлежала плоскости 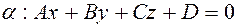необходимо, чтобы выполнялись условия:

1) , то есть ;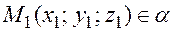

2) 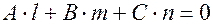( 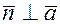, то есть ).

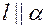Определение.Совокупность всех прямых, проходящих через данную точку 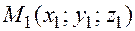, называется связкой прямых (с центром в точке ).

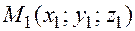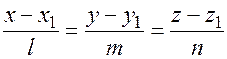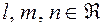Уравнение связки прямых: , где (и ).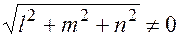

Пример. Дано общее уравнение прямой: 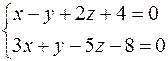, нужно найти каноническое уравнение этой прямой.

Решение. 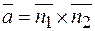, , 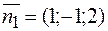, 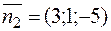значит 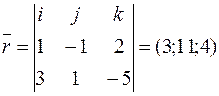. Найдем точку, принадлежащую , полагая что 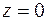, 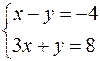следует, 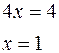, , 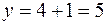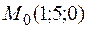принадлежит , следовательно, .

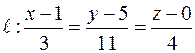Некоторые задачи на прямую и плоскость в пространстве.

Задача 1.Найти условие пересечения трех плоскостей 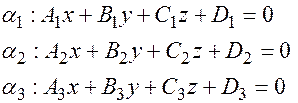в одной и только одной точке.

Чтобы три плоскости 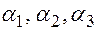пересекались в одной точке необходимо и достаточно, чтобы выполнялось условие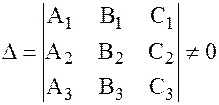

Задача 2.Записать уравнение прямой, проходящей через данную точку 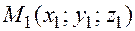и перпендикулярную данной плоскости (рис. 9.6)

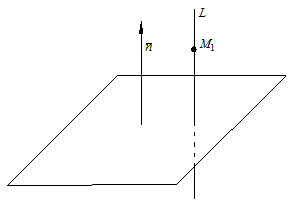
Рис. 9.6

Искомая прямая имеет вид .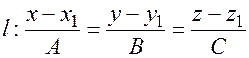

Задача 3.Записать уравнение плоскости, проходящей через прямую 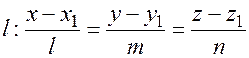и точку 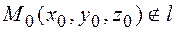(рис. 9.7).

Рис. 9.7

1) находим нормальный вектор для нашей плоскости ;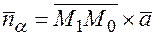

2) используя точку 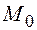и найденный нормальный вектор 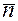, записываем общее уравнение плоскости ..

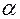Задача 4. Найти расстояние от точки 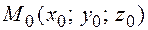до плоскости (рис 9.8) .

Поскольку расстояние от точки до плоскости есть проекция вектора соединяющего эту точку и любую точку на плоскости на нормальный вектор плоскости, поэтому ,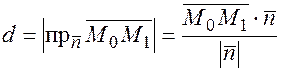

.

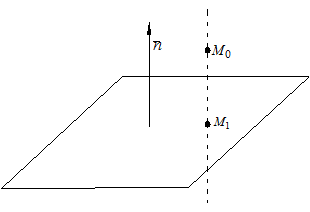
Рис. 9.8

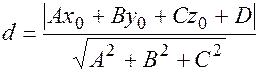(9.6)

Задача 5.Найти расстояние от точки 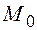до прямой 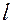(рис. 9.10).

Пусть прямая имеет вид 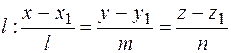, поскольку верна формула 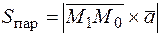, т. к. расстояние от точки 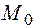до прямой 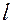есть высота параллелограмма построенного на векторах 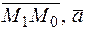, тогда .

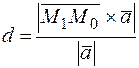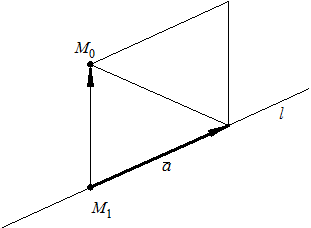
Рис. 9.10

Задача 6.Найти расстояние между двумя скрещивающимися прямыми (рис. 9.11).

Напомним, что две прямые называются скрещивающимися, если они не принадлежат одной плоскости.

Алгоритм действий при решении данной задачи может быть следующим:

1) проверяем, являются ли прямые скрещивающимися, для этого достаточно проверить будут ли направляющие векторы прямых и вектор, соединяющий две произвольные точки, принадлежащие прямым, компланарны, т.е. 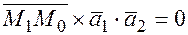. Если смешанное произведение равно нулю, то прямые не являются скрещивающимися и наоборот, если 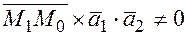, тогда прямые скрещивающиеся;

2) расстояние между скрещивающимися прямыми равно высоте параллелепипеда построенного на векторах 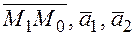, находим 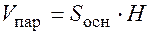тогда расстояние можно вычислить по формуле: .

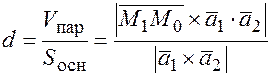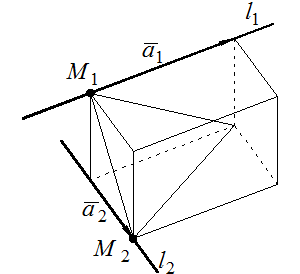
Рис. 9.11