Свойства умножения матрицы на число
1)  дистрибутивность относительно суммы числовых множителей;
дистрибутивность относительно суммы числовых множителей;
2) 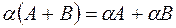 дистрибутивность относительно суммы матриц;
дистрибутивность относительно суммы матриц;
3)  ассоциативность относительно числового множителя;
ассоциативность относительно числового множителя;
4) 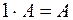 ;
;
5) 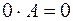 ;
;
Определение.Матрица 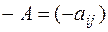 , (
, ( 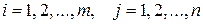 ) называется противоположной матрице
) называется противоположной матрице 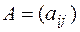 , (
, ( 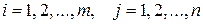 ).
).
Определение.Произведением матриц 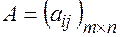 и
и 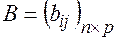 , называется матрица:
, называется матрица:
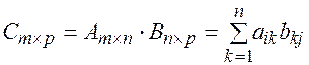 (10.3)
(10.3)
размерности ( 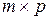 ).
).
Из формулы 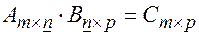 видно, что матрицы перемножаются только в том случае, когда число столбцов первой матрицы, совпадает с числом строк второй матрицы.
видно, что матрицы перемножаются только в том случае, когда число столбцов первой матрицы, совпадает с числом строк второй матрицы.
Формулу (10.3) можно рассматривать как совокупность скалярных произведений вектор-строк матрицы 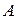 на вектор-столбцы матрицы
на вектор-столбцы матрицы 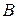 .
.
Замечание. Каждый элемент матрицы 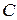 равен сумме произведений соответствующих элементов строки матрицы
равен сумме произведений соответствующих элементов строки матрицы 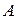 , на столбец матрицы
, на столбец матрицы 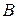 . Соответственно количество столбцов матрицы
. Соответственно количество столбцов матрицы 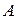 должно совпадать с количеством строк матрицы
должно совпадать с количеством строк матрицы 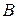 .
.
Дата добавления: 2015-08-26; просмотров: 744;
