РАНГ МАТРИЦЫ
Пусть дана прямоугольная матрица :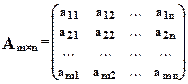 
.
Минором k -го порядка будем называть определитель, полученный из нее после вычеркивания (m-k) строк и (n-k) столбцов.
Минорами первого порядка являются элементы матрицы.
Наибольший порядок минора, который можно составить равен min {m, n}.
Рангом матрицы будем называть наибольший порядок отличного от нуля минора.
Из определения следует, что ранг невырожденной квадратной матрицы n -го порядка равен n, а ранг любой нулевой матрицы равен 0.
Базисными будем называть все миноры, отличные от нуля, порядок которых равен рангу матрицы.
Строки и столбцы матрицы ,входящие в базисный минор, будем называть базисными, а остальные ряды - свободными.
Элементарными преобразованиями матрицы назовем следующие операции:
- транспонирование;
- перестановки параллельных рядов (строк или столбцов);
- вычеркивание нулевого ряда;
- вычеркивание всех кроме одного одинаковых или пропорциональных
параллельных рядов;
- умножение любого ряда на число, не равное нулю;
- прибавление к любому ряду линейной комбинации параллельных рядов.
4.1. Элементарные преобразования не изменяют ранга матрицы.
4.2. Если ранг матрицы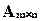 
равен r, то в ней можно найти ровно r линейно независимых строк
и столько же линейно независимых столбцов, при этом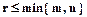 
.
4.3. Любой ряд матрицы можно представить в виде линейной комбинации параллельных базисных рядов.
4.4. Для того чтобы определитель квадратной матрицы был равен нулю, необходимо и достаточно,
Дата добавления: 2015-08-26; просмотров: 723;