Алгоритм вычисления обратной матрицы.
1. Находим определитель |A|. Если │А│≠ 0,то обратная матрица существует.
2. Составляем матрицу из алгебраических дополнений матрицы А.
А11 А12 А13
А = А21 А22 А23
А31 А32 А33
3. Полученную матрицу транспонируем
А11 А21 А31
А12 А22 А32 = Ã
А13 А23 А33
Назовём эту матрицу присоединённой.
4. Все элементы присоединённой матрицы делим на определитель |A|.
│А-1│=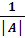 
* Ã
Проверка. Если │А-1│=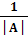 
* Ã = Е, то обратная матрица найдена верна
Пример. Найдем обратную матрицу, если
4 -8 -5
А = -4 7 -1
-3 5 1
1. 4 -8 -5 24 -43 0
|А| = -4 7 -1 = -4 7 -1 = 24*12- 7*43 = 288 – 301 = -13 -3 5 1 -3 5 1-3 5 1 -7 12 0
-7 12
2. 7 -1 -4 -1
А11 = = 7 + 5 = 12, А12 = - = 7, А13 = 1,
5 1 -3 1
-8 -5 4 -5
А21 = - = -17, А22 = = -11, А23= 4,
5 1 -3 1
А31 = 43, А32= 24 А33= - 4
12 7 1
-17 -11 4 ;
43 24 -4
3.12 7 1
à = -17 -11 4 ;
43 24 -4
4.Обратная матрица
- 
- 
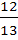
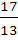А-1 = -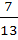 
- 
- 
- 
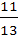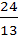
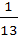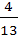
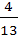
Дата добавления: 2015-08-21; просмотров: 1131;