Побочная диагональ главная диагональ
.
Квадратную матрицу будем называть треугольной, если все элементы, расположенные выше (либо ниже) главной диагонали равны нулю.
.
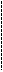
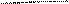
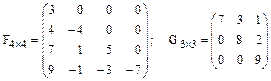Квадратную матрицу будем называть диагональной, если все ее элементы, нерасположенные на главной диагонали равны нулю.
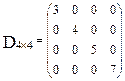- диагональная матрица четвертого порядка.
Диагональную матрицу будем называть единичной, если все элементы главнойдиагонали равны 1.
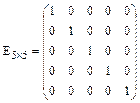- единичная матрица пятого порядка.
Элементы двух матриц будем называть соответствующими, если они имеют одинаковые индексы. Строки (столбцы) будем называть соответствующими, если они имеют одинаковый номер.
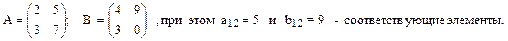
Транспонированием матрицы будем называть операцию замены всех столбцовсоответствующими строками
(всех строк соответствующими столбцами).
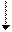
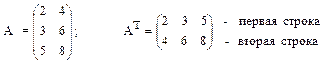
второй столбец
первый столбец
Матрицу будем называть симметрической (симметричной), если при транспонировании она не изменяется.
Из определения следует:
- симметрическая матрица может быть только квадратной;
- ее элементы расположены симметрично относительно главной диагонали.
.
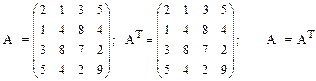Две матрицы одинаковой размерности будем называть равными , если все их соответствующие элементы равны.
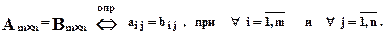
1.2. Действия с матрицами
Суммой двух матриц одинаковой размерности(А + В) будем называтьновую матрицу ( Х )той же размерности , каждый элемент которой равен сумме соответствующих элементов матриц-слагаемых.
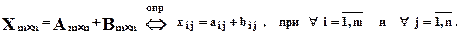
Произведением матрицы А на скаляр l ( l× А )будем называтьновую матрицу ( Х )той же размерности, каждый элемент которой равен произведению соответствующего элемента данной матрицы на данный скаляр.
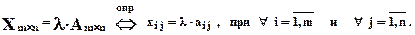
Из последних двух определений следует что разность двух матриц может быть найдена следующим образом:
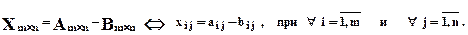
Скалярным произведением двух строк (или двух столбцов, или строки и столбца), имеющих одинаковое количество элементов, будем называть число, равное сумме произведений всех соответствующих элементов.
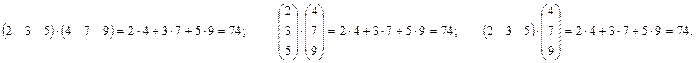
Линейной комбинацией строк (столбцов) будем называть сумму произведений этих строк (столбцов) на вещественные числа (скаляры).
Сами числа при этом называют коэффициентами этой линейной комбинации.
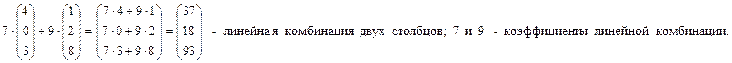
Произведением двух матриц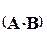 
будем называть новую матрицу 
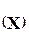, у которой каждый элемент хijравен скалярному произведению i - ойстроки первого сомножителя на j -й столбец второго сомножителя.
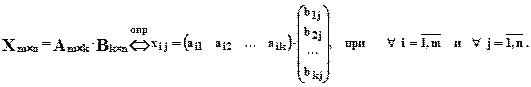
Из определения следуют свойства:
1.2.1. Количество столбцов матрицы-множимого должно быть равно количеству строк матрицы-множителя;
1.2.2. Матрица-произведение имеет столько строк, сколько их у матрицы-множимого и столько столбцов, сколько их у матрицы-множителя.
1.2.3. Умножение матриц не подчиняется переместительному закону.
1.2.4. Квадратные матрицы можно умножать только, если они имеют одинаковый порядок.
1.2.5. Умножение квадратной матрицы на единичную матрицу и слева и справа не изменяет данную матрицу.
; 
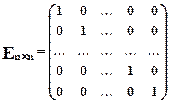
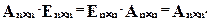
Две квадратные матрицы будем называть взаимно обратными, если их произведение равно единичной матрице.
Взаимно обратные матрицы обычно обозначают так: АиА-1.
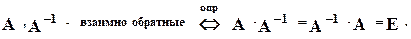
Дата добавления: 2015-08-26; просмотров: 879;