НЕОПРЕДЕЛЕННЫЕ ЛИНЕЙНЫЕ АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Рассмотрим случай, когда 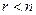 :
:
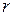 переменных называют основными (или базисными), если определитель матрицы, составленный из коэффициентов при них (т.е. базисный минор) отличен от 0.
переменных называют основными (или базисными), если определитель матрицы, составленный из коэффициентов при них (т.е. базисный минор) отличен от 0.
Остальные 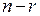 называются неосновными (или свободными).
называются неосновными (или свободными).
Для наилучшего понимания решения подобных систем рассмотрим систему:

Выпишем расширенную матрицу системы и преобразуем ее:

Откуда видно, что 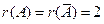 , но
, но 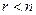 , т.к.
, т.к. 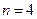 , т.е. система неопределена и имеет бесконечно много решений. Найдем их:
, т.е. система неопределена и имеет бесконечно много решений. Найдем их:
Базисный минор, отличный от нуля 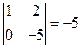 при неизвестных
при неизвестных 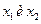 , их мы и берем за основные (базисные) переменные. Остальные
, их мы и берем за основные (базисные) переменные. Остальные  будут неосновными переменными, которые мы перенесем в правые части уравнений. В результате имеем
будут неосновными переменными, которые мы перенесем в правые части уравнений. В результате имеем
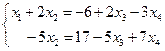
Откуда
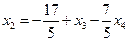
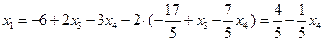 .
.
Придавая неосновным переменным произвольные значения,
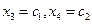 ,где
,где 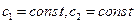
найдем бесконечное множество решений системы
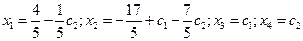 ,где
,где 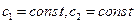
Дата добавления: 2015-08-21; просмотров: 613;
