Разложим функцию в степенной ряд Тейлора в рабочей точке А

.

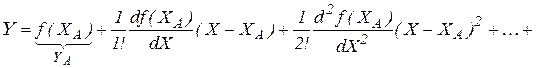
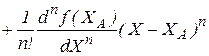При рассмотрении изменения X в окрестностях точки А в неболь­шом диапазоне возможно ограничиться рассмотрением 2-х первых членов ряда Тейлора

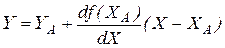
	X – XA = ΔX – отклонение X от исходного значения;
Y – YA = ΔY – отклонение Y от исходного значения.

Тогда ,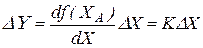

где 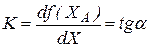– коэффициент связи между У и X в окрестностях точки А или коэффициент усиления элемента в окрестности исходной точки.

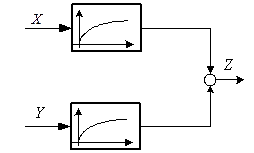
На структурной схеме последнее уравнение изобразится:

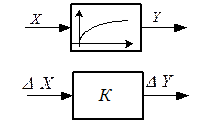
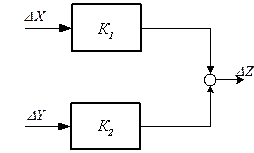
б) Функция двух переменных.

Пусть дана статическая характеристика в виде непрерывной дифференцируемой функции двух переменных

Z = f(X,Y)

Точкой основного режима работы является точка А.

Разложим функция в степенной ряд Тейлора в точке А:

.

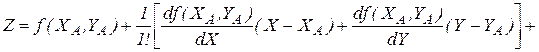
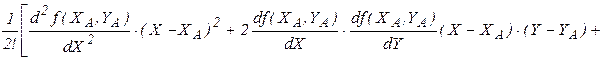
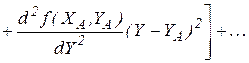При небольшом отклонении Х, У от рабочей точки А также допустимо ограничение двумя членами ряда Тейлора

.

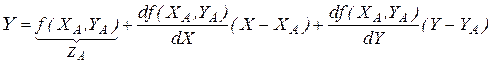Обозначим

,

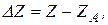
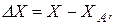
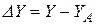тогда последующее уравнение

.