Построение переходных функций и ЛАЧХ фазовойой системы (3 стр. 17-19)

Во всех рассмотренных случаях наблюдается однозначная зависимость между формой ЛАЧХ и ЛФЧХ звеньев. Такие звенья и САУ, состоящая из этих звеньев, называются минимально-фазовыми.

При сопоставлении ЛАЧХ и соответствующих им переходных функций можно убедиться в следующем:

1) установившееся значение выходной величины определяется ординатой ЛАЧХ L(0) при нулевой частоте, т.е. X¥ = 10L(0);

2) начальное значение выходной величины определяется ординатой ЛАЧХ при w = ¥, т.е. X(0) = 10L(¥);

3) переходный процесс протекает без перерегулирования, если ординаты ЛАХ на всех частотах не превышают ординаты ЛАХ при нулевой частоте;

максимум Lm в ЛАХ свидетельствует о том, что переходный процесс протекает с перерегулированием. Максимальное отклонение выходной величины приблизительно равно входному сигналу, умноженному на максимальное значение коэффициента усиления АЧХ (Km=10Lm);

4) переходный процесс до достижения максимума протекает приблизительно по экспоненте, сдвинутой на время постоянного запаздывания. Экспонента имеет постоянную времени, которая определяется изменением наклона ЛАХ с нулевого (0) на единичный отрицательный (–1). Время постоянного запаздывания равно сумме постоянных времени, определяющих дальнейшее увеличение отрицательного наклона ЛАХ в области высоких частот;

5) переходный процесс после достижения максимума идёт приблизительно по экспоненте с постоянной времени, которая определяется изменением наклона аппроксимированной ЛАХ с единичного положительного (+1) на нулевой (0).

Определение показателей регулирования по результирующей ЛАЧХ минимально-фазовой САУ основано на построении приближённой кривой переходного процесса. При этом можно рекомендовать следующую методику:

1) построить аппроксимированную отрезками прямых с наклонами 1, 0, -1,-2, -3,… лог/дек результирующую ЛАЧХ системы. При этом будут получены аппроксимированные ЛАЧХ типа 1, 2,3 (рис.1);

2) определить частоты точек сопряжения отрезков с +1 и 0 наклоном , с 0 и –1 наклонами , с –1 и –2 наклонами и т.д.;

3) определить значения амплитуд, соответствующих максимальным и установившимся значениям ЛАЧХ ;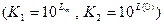

4) на оси времени кривой переходного процесса (рис.1) отложить отрезок, соответствующий 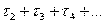, и из полученной точки на прямую К1 отложить подкасательную 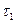и соответствующей кривой нарастания X экспоненту;

5) для ЛАЧХ типа 1 кривая переходного процесса 1 может быть получена путём плавного перехода из начала координат на полученную экспоненту;

6) для ЛАЧХ типа 2 и 3 необходимо построить экспоненту с подкасательной , соответствующую спадающему участку кривой переходного процесса. Результирующая кривая 2, 3 переходного процесса может быть получена путём плавного перехода с нарастающего участка на экспоненту, соответствующую спадающему участку кривой переходного процесса до установившегося значения (К2 , 0).

Переходный процесс может быть построен, если САУ представить эквивалентным колебательным звеном второго порядка. При этом частота (период ТК = 2p/wK) и постоянная затухания зависят от коэффициента демпфирования x. По аналогии с колебательным звеном x может быть определён высотой g всплеска ЛАЧХ типа L (рис.7 б), т.е. 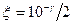. Построение приближённой кривой переходного процесса (рис.7 г) сводится к построению огибающих с подкасательной Тз и вписанных между огибающими колебаний X c периодом ТК.

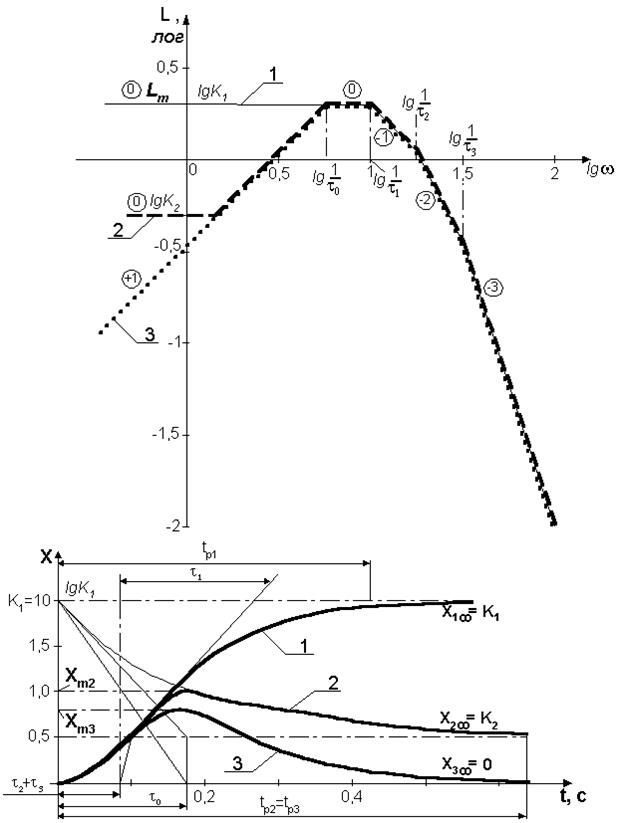
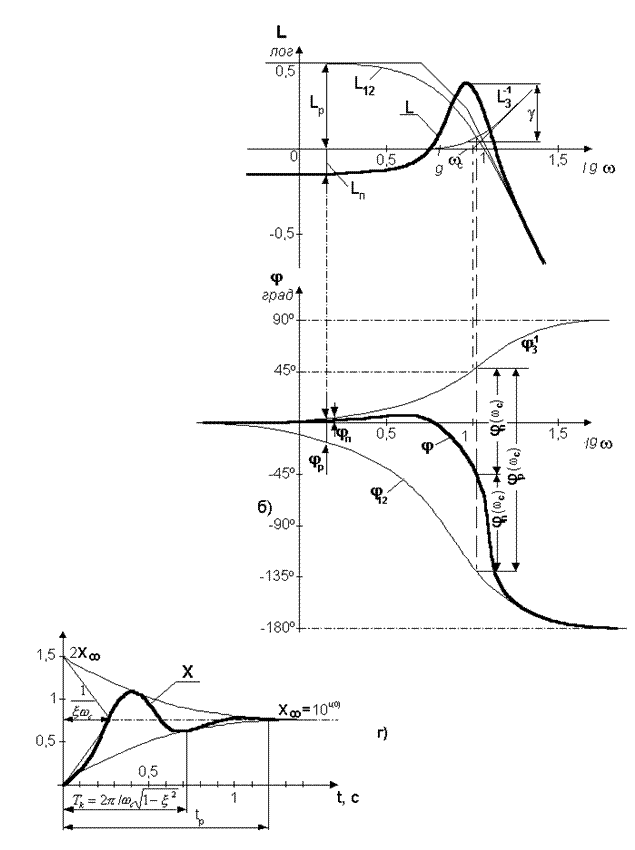
Рис.1 ЛАЧХ и переходные функции при различных САУ