Геометрический и механический смысл производной

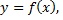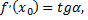Если кривая задана уравнением то где 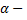угол, образованный с положительным направлением оси 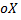касательной к кривой в точке с абсциссой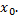

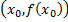Касательной к графику функции в заданной точке называют предельное положение секущей при 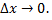Если функция 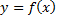имеет в точке производную, то существует касательная к графику функции 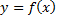в точке 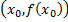, причем угловой коэффициент этой касательной равен производной 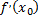. Уравнение касательной к кривой 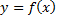в точке 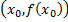имеет вид

.

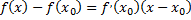Нормалью к кривой называется прямая, перпендикулярная касательной и проходящая через точку касания. Уравнение нормали имеет вид

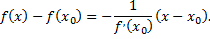
Угол между двумя кривыми 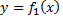и в точке их пересечения 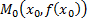называется угол между касательными к этим кривым в точке Этот угол находится по формуле

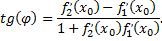
Предположим, что функция 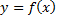описывает закон движения материальной точки 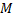по прямой линии, т.е. 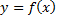– путь пройденной точкой 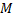от начала отсчета за время

Тогда за время пройден путь 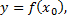а за время 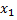– путь За промежуток времени 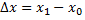точка 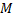пройдет отрезок пути

.

Отношение 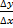называется средней скоростью движения за время , а предел отношения 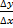при 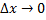определяет мгновенную скорость точки в момент времени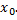

Рассмотрим пример. Тело, подброшенное вертикально вверх, движется по закону

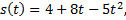
где высота 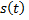измеряется в метрах, а время 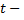в секундах. Найти: 1) скорость тела в начальный момент; 2) скорость тела в момент соприкосновения с землей; 3) наибольшую высоту подъема тела.

1) Скорость тела в момент 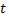равна производной , т.е.

в момент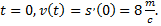

2) В момент соприкосновения с землей т.е.

Решая данное уравнение, получим корни данного уравнения

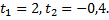
Второй корень уравнения не подходит по смыслу, так как время – величина положительная. Найдем скорость тела в момент времени (скорость тела в данный момент времени противоположна направлению начальной скорости).

3) Наибольшая высота подъема 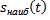будет в момент, когда скорость тела равна 0 и происходит переход от подъема к падению тела, т.е. 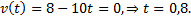Наибольшая высота подъема

Значение производной состоит в том, что при изучении любых процессов и явлений природы с ее помощью можно оценить скорость изменения связанных между собой величин.