Основные правила дифференцирования. Рассмотрим основные правила дифференцирования.
Рассмотрим основные правила дифференцирования.
Если функции 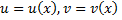 дифференцируемы в точке
дифференцируемы в точке  , то сумма, разность, произведение и частное этих функций (частное при условии, что
, то сумма, разность, произведение и частное этих функций (частное при условии, что 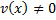 ) также дифференцируемы в этой точке и имеют место следующие формулы:
) также дифференцируемы в этой точке и имеют место следующие формулы:
1) 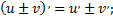
2) 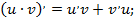
3) 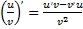 ;
;
4) 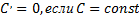 .
.
Если 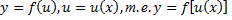 (сложная функция) где функции
(сложная функция) где функции  имеют производные, то правило дифференцирования данной функции следующее
имеют производные, то правило дифференцирования данной функции следующее

Формулы дифференцирования основных функций (табл. 5).
Таблица 5
| Функция | Производная функции | Функция | Производная функции |
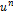
| 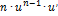
| 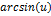
| 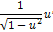
|

| 
| 
| 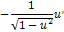
|
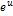
| 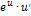
| 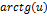
| 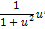
|
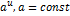
| 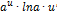
| 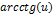
| 
|
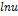
| 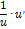
| 
| 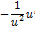
|
| Функция | Производная функции | Функция | Производная функции |
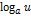
| 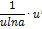
| 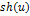
| 
|
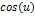
| 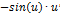
| 
| 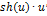
|
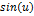
| 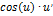
| 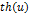
| 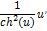
|
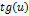
| 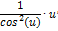
| 
| 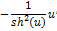
|
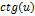
| 
| 
| 
|
Рассмотрим примеры на применение правил дифференцирования.
1) 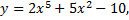
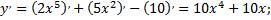
2) 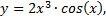
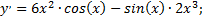
3) 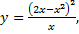
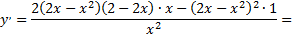
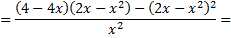
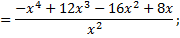
4) 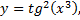
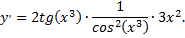
Дата добавления: 2015-08-11; просмотров: 654;
