Определение функции многих переменных. Область определения функции многих переменных
Если множество 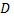 рассматривать как множество точек
рассматривать как множество точек 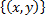 на плоскости и каждой точке
на плоскости и каждой точке 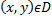 поставить в соответствие определенное число
поставить в соответствие определенное число 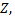 то, тем самым, на множестве
то, тем самым, на множестве 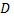 определяется функция
определяется функция 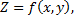 которую называют функцией двух переменных.
которую называют функцией двух переменных.
Геометрической интерпретацией функции двух переменных служит поверхность
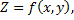
которую называют графиком этой функции.
Подобным образом можно определить функцию трех переменных.
Для определения функций большого числа переменных потребуется рассматривать пространства размерности 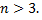
Определение 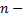 мерного арифметического пространства
мерного арифметического пространства 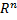 : множество всех упорядоченных совокупностей по
: множество всех упорядоченных совокупностей по 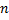 действительных чисел
действительных чисел 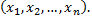
Элементы этого множества называют точками 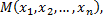 а числа
а числа 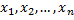 - их координатами.
- их координатами.
Если каждой точке 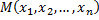 из множества
из множества 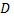 точек пространства
точек пространства 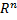 поставлено в соответствие по некоторому закону число
поставлено в соответствие по некоторому закону число 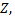 то на множестве
то на множестве 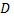 определена функция
определена функция  переменных
переменных
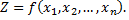
Рассмотрим примеры функций двух переменных.
Например, функция
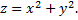
Область определения этой функции – множество всех пар чисел 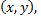 т.е. вся плоскость
т.е. вся плоскость  а множество значений – промежуток
а множество значений – промежуток 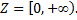
Функция

Областью определения данной функции является множество всех точек, для которых выражение  определено, т.е. множество точек, для которых
определено, т.е. множество точек, для которых
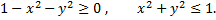
Множество всех таких точек образует круг с центром в начале координат и радиусом, равным единице. Множество значений функции представляет собой отрезок 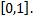
Из рассмотренных примеров следует, что областью определения двух переменных может быть вся плоскость 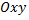 или ее часть.
или ее часть.
Число  называется пределом функции
называется пределом функции 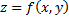 в точке
в точке 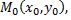 если для любого
если для любого 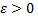 существует
существует 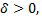 такое, что при всех
такое, что при всех  удовлетворяющих условиям
удовлетворяющих условиям
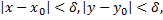
справедливо неравенство
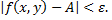
Если  предел функции
предел функции 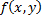 в точке
в точке 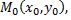 то
то
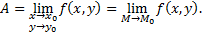
Функция 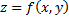 называется непрерывной в точке
называется непрерывной в точке 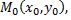 если справедливо равенство
если справедливо равенство
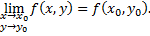
Например, функция
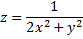
непрерывна в любой точке плоскости, за исключением точки 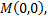 в которой функция терпит бесконечный разрыв.
в которой функция терпит бесконечный разрыв.
Функция, непрерывная во всех точках некоторой области 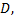 называется непрерывной в данной области.
называется непрерывной в данной области.
Если переменной  дать некоторое приращение
дать некоторое приращение 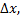 а
а  оставить постоянной, то функция
оставить постоянной, то функция 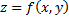 получит приращение
получит приращение 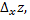 называемое частным приращением функции
называемое частным приращением функции 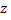 по переменной
по переменной 
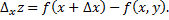
Аналогично, если переменная  получает приращение
получает приращение 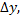 а
а  остается постоянной, то частное приращение функции
остается постоянной, то частное приращение функции 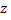 по переменной
по переменной 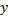
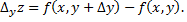
Дата добавления: 2015-08-11; просмотров: 1352;
