Частные производные и дифференциалы первого и высших порядков
Если существуют пределы

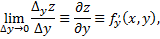
они называются частными производными функции 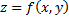 по переменным
по переменным  и
и  соответственно.
соответственно.
Аналогично определяются частные производные функций любого числа переменных.
Так как частная производная по любой переменной является производной по этой переменной, найденной при условии, что остальные переменные – постоянны, то все правила и формулы дифференцирования функции одной переменной применимы для нахождения частных производных функций любого числа переменных.
Рассмотрим примеры.
1)Найти частные производные функции
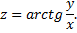
Частная производная по переменной  :
:
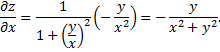
Частная производная по переменной 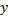 :
:
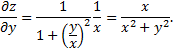
2)Найти частные производные функции
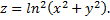
Частная производная по переменной  :
:
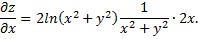
Частная производная по переменной 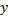 :
:
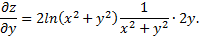
Дифференциал функции 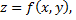 найденный при условии, что одна из независимых переменных изменяется, а вторая остается постоянной, называется частным дифференциалом, т.е. по определению
найденный при условии, что одна из независимых переменных изменяется, а вторая остается постоянной, называется частным дифференциалом, т.е. по определению

где 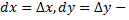 произвольные приращения независимых переменных, называемые их дифференциалами. Это справедливо и для функции трех переменных
произвольные приращения независимых переменных, называемые их дифференциалами. Это справедливо и для функции трех переменных 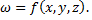
Вычислить значения частных производных функции
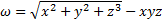
в точке 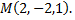
Находим частные производные
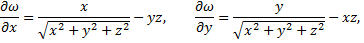
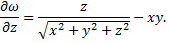
В полученные выражения подставляем координаты данной точки
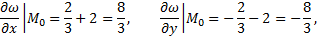
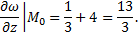
Полным приращением функции 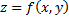 называется разность
называется разность
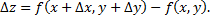
Главная часть полного приращения функции 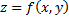 , линейно зависящая от приращений независимых переменных
, линейно зависящая от приращений независимых переменных 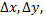 называется полным дифференциалом функции и обозначается
называется полным дифференциалом функции и обозначается 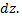
Если функция имеет непрерывные частные производные, то полный дифференциал существует и равен
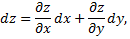
где 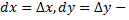 произвольные приращения независимых переменных, называемые их дифференциалами.
произвольные приращения независимых переменных, называемые их дифференциалами.
Рассмотрим пример.
Найти полный дифференциал функции
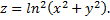
Найдем частные производные
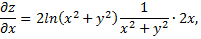
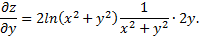
Полный дифференциал
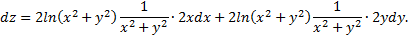
Полный дифференциал часто используется для приближенных вычислений значений функции, так как
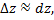
т.е.
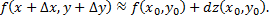
Рассмотрим пример.
Вычислить приближенно 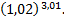
Рассмотрим функцию 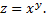 При
При  имеем
имеем 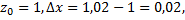
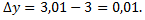
Найдем полный дифференциал функции 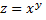 в любой точке
в любой точке
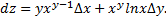
Вычислим его значение в точке 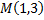 при данных приращениях
при данных приращениях 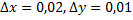
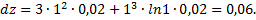
Тогда

Функция 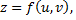 где
где 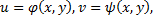 называется сложной функцией переменных
называется сложной функцией переменных 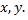 Для нахождения частных производных сложных функций используются формулы
Для нахождения частных производных сложных функций используются формулы
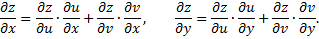
В случае, когда 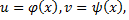 формула преобразуется к виду
формула преобразуется к виду
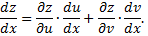
Если же 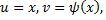 то формула имеет вид
то формула имеет вид
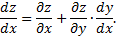
Рассмотрим пример.
Найти частные производные функции

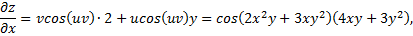
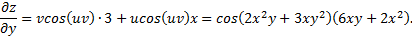
Если уравнение 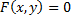 задает некоторую функцию
задает некоторую функцию 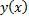 в неявном виде и
в неявном виде и 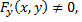 то
то
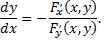
Если уравнение 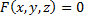 задает функцию двух переменных
задает функцию двух переменных 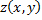 в неявном виде и
в неявном виде и 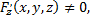 то справедливы формулы
то справедливы формулы
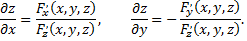
Рассмотрим пример. Найти производную функции 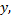 заданной неявно уравнением
заданной неявно уравнением
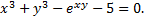
Согласно формуле
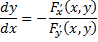
получим
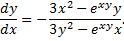
Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка
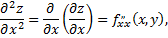
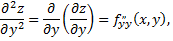
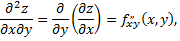
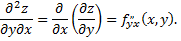
Дата добавления: 2015-08-11; просмотров: 1544;
