Касательная плоскость и нормаль к поверхности. Если поверхность задана уравнением то уравнение касательной плоскости в точке к данной поверхности

Если поверхность задана уравнением 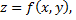то уравнение касательной плоскости в точке 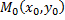к данной поверхности

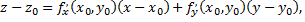
а каноническое уравнение нормали, проведенной через точку 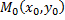поверхности

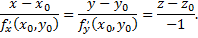
В случае, когда уравнение поверхности задано в неявном виде

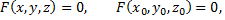
то уравнение касательной плоскости в точке имеет вид

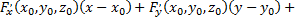
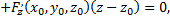
а уравнение нормали

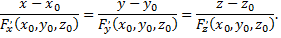
Рассмотрим пример.

Найти уравнение касательной плоскости и нормали к поверхности

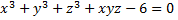
в точке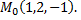

Необходимо вычислить значения частных производных в заданной точке

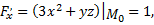
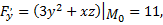
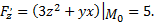
Подставив в формулу уравнения касательной плоскости, получим уравнение

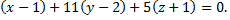
Подставив в формулу уравнения нормали плоскости, получим уравнение

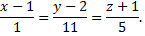
Точка 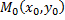называется точкой локального максимума (минимума) функции

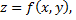если для всех точек 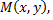отличных от 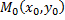и принадлежащих достаточно малой окрестности, выполняется неравенство

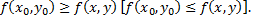
Максимум или минимум функции называется ее экстремумом. Точка, в которой достигается экстремум функции, называется точкой экстремума функции.