Метод множителей Лагранжа

Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.

Рассмотрим функцию трех переменных

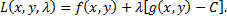
Эта функция называется функцией Лагранжа, а 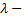множителем Лагранжа.

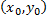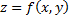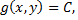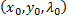Если точка является точкой условного экстремума функции при условии то существует значение такое, что точка является точкой экстремума функции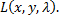

Для нахождения условного экстремума функции 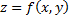при условии 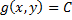требуется найти решение системы

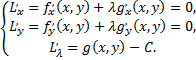
Последнее из уравнений системы совпадает с уравнением связи.

В точке условного экстремума линия уровня функции 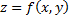касается линии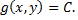

Рассмотрим пример. Найти точки экстремума функции при условии

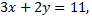используя метод множителей Лагранжа.

Составим функцию Лагранжа

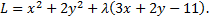
Приравнивая к нулю ее частные производные, получим систему уравнений

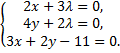
Ее единственное решение 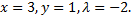Таким образом, точкой условного экстремума может быть только точка 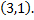Нетрудно убедиться в том, что эта точка является точкой условного минимума.

Во многих задачах критическая точка функции Лагранжа оказывается единственной и соответствует не только локальному, но и глобальному условному минимуму или максимуму.

Контрольные вопросы

1. Записать уравнение касательной плоскости и нормали к поверхности.

2. Сформулировать необходимое и достаточное условия экстремума функции двух переменных.

3. Сформулировать суть метода множителей Лагранжа.

4. Как находят наибольшее и наименьшее значения функции на замкнутом множестве?