Интегрирование методом замены переменной

Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т.е. перейти к непосредственному интегрированию. Такой метод называют методом подстановки или методом замены переменной.

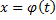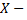Данный метод основан на теореме: пусть функция определена и дифференцируема на некотором промежутке и пусть множество значений этой функции, на котором определена функция . Тогда на множестве функция имеет первообразную, на множестве справедлива формула

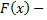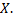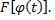Пусть первообразная для на множестве Рассмотрим на множестве сложную функцию По правилу дифференцирования сложной функции, учитывая, что

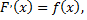
получаем

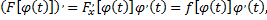
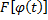т.е. функция имеет на множестве первообразную , следовательно

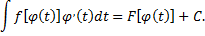
Замечая, что

.

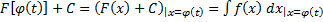Рассмотрим пример. Найти неопределенный интеграл

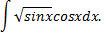
Сделаем замену Получим

Рассмотрим еще один пример. Найти интеграл

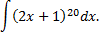
Сделаем замену 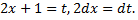Получим

Пример. Найти интеграл

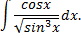
Сделаем замену 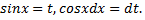Получим

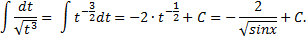
Рассмотрим пример. Найти интеграл и проверить ответ дифференцированием

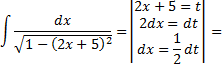
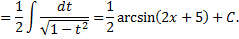
Проверим

Рассмотрим пример. Найти интеграл и проверить ответ дифференцированием

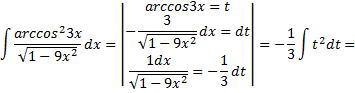
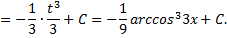
Проверим

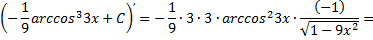
Рассмотрим пример. Найти интеграл

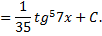
Рассмотрим пример. Найти интеграл

Контрольные вопросы

1. Какая функция называется первообразной?

2. Что представляет собой неопределенный интеграл?

3. Какими свойствами обладает неопределенный интеграл?

4. Какова идея метода замены переменной?