Анализ АИТ методом основной гармоники.

Из-за наличия в схеме трех накопителей энергии: L_d, C, L_н, теоретический анализ схемы имеет определенную трудность, в связи с чем здесь наибольшее применение получил так называемый метод основной гармоники, обладающий наглядностью и удобством в изучении процессов. Применительно к инвертору этот метод основывается на замене кривых напряжения на нагрузке U_н и тока инвертора i_и их первыми (основными) гармониками. Такая замена создает некоторую погрешность в расчётах, однако, как показывает эксперимент, она не превышает 10-15%. Для трехфазных АИТ, где указанные кривые меньше отличаются от синусоиды, точность расчетных соотношений получается выше. Важным достоинством метода основных гармоник является возможность применения векторных диаграмм для анализа режимов работы и характеристик АИТ.

В АИТ индуктивность входного дросселя L_d обычно велика, поэтому при анализе методом основной гармоники принимают L_d=∞. При таком предположении ток i_d получается идеально сглаженным, а кривые токов тиристоров и инвертора имеют прямоугольную форму. Кривые напряжения на нагрузке U_н и тока инвертора i_и с учетом этих допущений имеют следующий вид (рисунок 1.2.а).

Первая гармоника тока инвертора i_и(1) связана с кривой тока i_и при L_d=∞ соотношением:

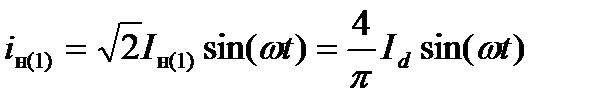(1.1)

где 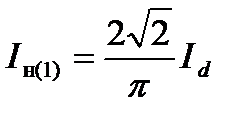- действующее значение первой гармоники тока инвертора.

I_d – ток во входной цепи.

Таким образом, приняв напряжение U_н(ωt) и ток i_и(ωt) синусоидальными, анализ инвертора можно проводить по схеме замещения для первой (основной) гармоники (рисунок 1.2.б) с использованием векторной диаграммы (рисунок 1.2.в). Вектор напряжения располагают по вертикальной оси. Ток I_н активно-индуктивной нагрузки отстает от вектора U_н на угол 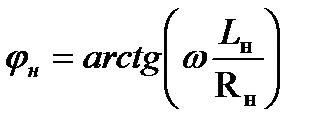. Вектор тока I_с опережает вектор напряжения U_н на 90°. Вектор I_н(1), равный сумме I_н + I_с, опережает вектор напряжения на угол Θ. Опережающий характер вектора I_н(1) является обязательным для АИТ, т.к. угол Θ определяет время, предоставляемое тиристорам для восстановления запирающих свойств.

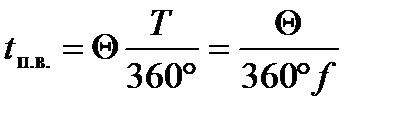(1.2)

где Т – период, f - выходная частота инвертора.

Угол Θ не может быть меньше величины Θ_min , которой соответствует минимально-допустимое значение t_п.в., равное времени выключения используемых тиристоров (t_в)

(1.3)

Для АИТ представляет наибольший интерес зависимость его выходного напряжения от тока нагрузки – выходная характеристика – определяемая в ходе дальнейшего анализа. Из векторной диаграммы определим проекцию вектора I_н(1) на вертикальную и горизонтальную оси:

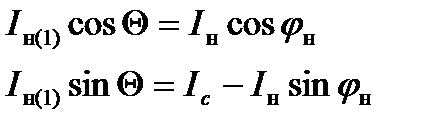(1.4)

Физический смысл уравнений (1.4) будет ясен, если умножить их левые и правые части на величину U_н. При этом первое выражение будет характеризовать закон сохранения активной энергии, а второе – реактивной. Активная энергия, отдаваемая инвертором потребляется сопротивлением нагрузки R_н, а реактивная энергия (мощность), потребляемая инвертором равна разности энергий (мощностей) генерируемой конденсатором и потребляемой нагрузкой. Необходимость в потреблении инвертором реактивной мощности связано с обеспечением угла Θ для запирания проводящих тиристоров. Разделив второе уравнение на первое, получим:

(1.5)

Введем обозначение 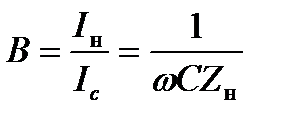(1.6)

Тогда: 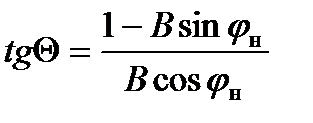(1.7)

Коэффициент В называют коэффициентом (факторам) нагрузки.

Воспользуемся уравнением баланса активной мощности в инверторе, согласно которому в отсутствие потерь вся энергия, потребляемая от источника питания, отдается в нагрузку.

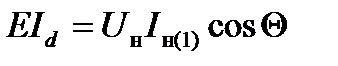(1.8)

Выразив I_н(1) через I_d получим выражение:

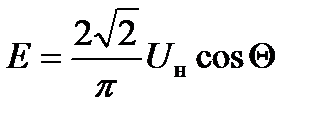(1.9)

Оно является частным случаем важнейшего для АИТ соотношения:

(1.10)

где 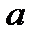_н – коэффициент, определяющий вид схемы инвертора.

Для однофазных схем с нулевым выводом и мостовой: ;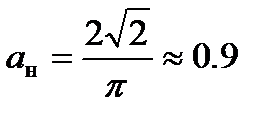

для трехфазной нулевой ;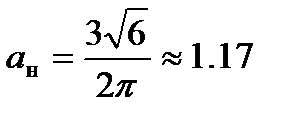

для трехфазной мостовой .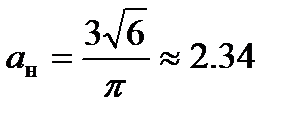

Для уравнения (1.10) напряжение на нагрузке инвертора:

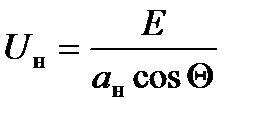(1.11)

Из уравнения (1.7):

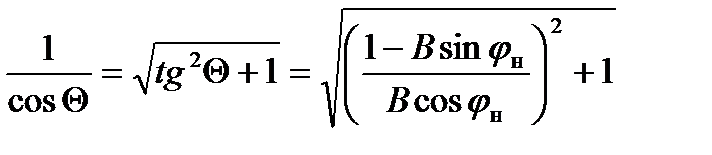(1.12)

Поскольку 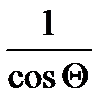зависит от параметров нагрузки R_н, L_н , то и U_н также оказывается зависимым от них. Соотношение (1.10) позволяет выявить важную для теории автономных инверторов зависимость:

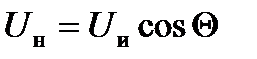(1.13)

где 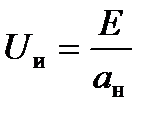- расчетное напряжение инвертора, зависящее только от напряжения питания

Е и вида схемы инвертора.

Указать напряжение U_н непосредственно на схеме нельзя, но им удобно пользоваться на векторных диаграммах, что оправдывает его введение. Из выражения (1.13) следует, что вектор напряжения U_н совпадает по направлению с вектором тока I_н(1). Геометрическим местом конца вектора U_н, например при изменении параметров нагрузки и стабилизации напряжения U_н путем регулирования напряжения Е будет окружность, построенная на векторе U_н как на диаграмме (рисунок 1.3).

Выражение, описывающее выходные характеристики АИТ находятся подстановкой (1.12) в (1.11):

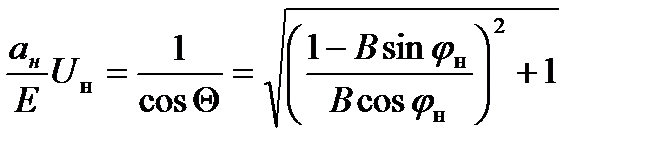(1.14)

Графически выходные характеристики изображаются в виде зависимости относительного напряжения на нагрузке 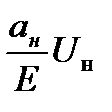от коэффициента нагрузки 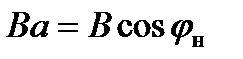при фиксированных значениях 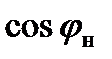(рисунок 1.4). Выходные характеристики АИТ с ростом коэффициента нагрузки, т.е. с увеличением тока нагрузки имеют падающий характер.

Рассмотрим выходную характеристику при 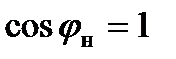, что соответствует чисто активной нагрузке и коэффициенту 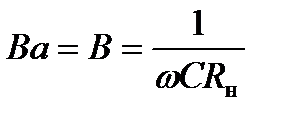. Примем величину емкости конденсатора, а также напряжение Е неизменными.

Кривые напряжения на нагрузке (конденсаторе) и на тиристоре инвертора для одной из точек средней области выходной характеристики ( 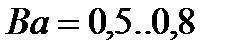) выглядят следующим образом (рисунок 1.5а). Вид кривых характеризуется экспоненциальным процессом перезаряда конденсатора С постоянной времени 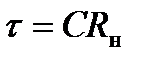. Напряжение на конденсаторе в начале и в конце каждого полупериода равны и противоположны по знаку, а средняя его величина на полупериоде равна Е.

При переходе в область малых значений коэффициента Ва (больших значений R_н и малых токов нагрузки), постоянная времени τ перезаряда конденсатора увеличивается (рисунок 1.5б), что ведет к увеличению угла Θ, стремящегося при Ва→0 к Т/4. Кривая напряжения на конденсаторе приближается к треугольной форме. Равенство среднего за полупериод напряжения величине Е достигается за счет увеличения амплитуды выходного напряжения. Этим объясняется повышение действующего значения напряжения на выходе инвертора при уменьшении тока нагрузки (рисунок 1.4). При переходе к режиму холостого хода (Ва→0), напряжение на выходе инвертора может выйти за пределы допустимого для нормальной работы элементов (конденсатора, тиристоров). Из-за опасности выхода из строя элементов схемы, вследствие перенапряжений, режима холостого хода рассматриваемого инвертора следует избегать.

При переходе инвертора в режим больших токов нагрузки (Ва>0,8) наблюдается обратное явление. Вследствие уменьшения величины R_н постоянная времени перезаряда конденсатора τ уменьшается, вызывая уменьшения угла Θ (рисунок 1.5в). Напряжение на выходе инвертора также уменьшается и приближается к прямоугольной форме с действующим значением, стремящемся к 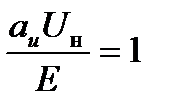. Однако режим 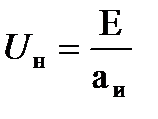для инвертора невозможен, поскольку угол Θ здесь равен нулю. Предел увеличения тока нагрузки характеризуется ординатой, для которой Θ=Θ_min . Из (1.14) получаем:

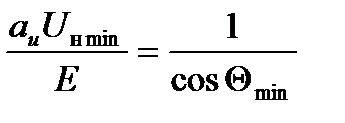, (1.15)

где Θ_min определяется по формуле (1.3).

Таким образом, из анализа схемы можно сделать вывод, что для рассмотренной схемы АИТ недопустим режим холостого хода и имеется предел увеличения тока нагрузки.

При активно-индуктивной нагрузке падающий характер выходных характеристик сохраняется и обуславливается теми же причинами, что и при активной нагрузке. Отличие лишь в том, что индуктивность нагрузки осуществляет некоторую компенсацию реактивности конденсатора, что приводит к уменьшению угла Θ и уменьшению выходного напряжения инвертора при тех же значениях параметра Ва. Этим объясняется смещение характеристик к оси ординат с уменьшением .