Метод геометрического суммирования напряжений.

Этот метод чаще всего используется, когда необходимо регулировать напряжение на нагрузке в широких пределах при значительной мощности (десятки – сотни киловатт). При использовании этого метода два инвертора включают параллельно по цепи постоянного тока и последовательно по цепи переменного тока, на рисунке 1.22 последовательно включены вторичные обмотки инверторных трансформаторов.

В этом случае результирующее напряжение на нагрузке равно геометрической сумме выходных напряжений каждого инвертора, а его величина зависит от фазового сдвига ψ между выходными напряжениями U_n1 и U_n2 первого и второго инверторов. При ψ=0 напряжение на нагрузке максимально U_н = U_{н max} (рисунок 1.23 а). При ψ=180° - минимально, U_н = U_{н min}, а если U_н1= U_н2, то U_н=0 (рисунок 1.23 б). При 0<ψ<180, U_{н min}< U_н < U_{н max} (рисунок 1.23 в).

Регулировка угла ψ осуществляется с помощью системы управления, при этом импульсы управления тиристорами второго инвертора сдвигаются по времени и по отношению к импульсам управления первого.

Этот принцип регулирования применим к любому АИТ, но наиболее целесообразен в многофазных системах, в которых в кривой выходного напряжения невелико содержание высших гармоник (чаще всего инвертор выполняется по 3-х фазной мостовой схеме).

При использовании этого принципа в однофазных системах необходимо предварительно отфильтровать высшие гармоники, а затем уже суммировать выходные напряжения. Особенно нежелательно наличие чётных гармоник в кривой выходного напряжения каждого инвертора. Например, при узле сдвига ψ₍₁₎ по первой гармонике в 180° для второй гармоники фазовый сдвиг ψ₍₂₎ = 360°, т.е. напряжения этой гармоники суммируются.

Чтобы обеспечить равномерное распределение нагрузки по инверторным мостам и получить чёткое геометрическое суммирование, необходимо стабилизировать выходное напряжение каждого из инверторов. Для этой цели может быть использован любой из рассмотренных нами способов стабилизации U_Н, например, как на схеме рисунок 25, с помощью обратного выпрямителя.

Рассмотрим векторную диаграмму для основной гармоники токов одной из фаз для анализа режимов работы такого АИТ (рисунок 1.24).

Предположим, что коэффициенты трансформации выпрямительных тиристоров n_в1=n_в2=n_в, следовательно:

cos θ = cos θ₁ = cos θ₂ = 1/ n_в (1.32)

U_u = U_н1 = U_н2 = E/a_н 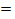Е· n_в/2,34 (1.33)

Величина n_в выбирается таким образом, чтобы обеспечить требуемое время t_п.в восстановления запирающих свойств тиристоров инверторов. Напряжения на вторичной стороне инверторных тиристоров:

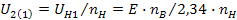(1.34)

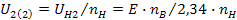(1.35)

Из векторной диаграммы находим:

δ = 180° - ψ (1.36)

Т.к. треугольник ОАВ равнобедренный, то

U_н/2 = U_u sin / n_н = cos(ψ/2) (1.37)

Откуда: U_u = 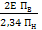cos 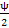= 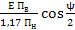(1.38)

Следовательно, регулируя угол фазового сдвига от 0 до 180° можно менять напряжение на нагрузке от U_{н max} до нуля.

Векторная диаграмма строится таким образом. Вектор тока I_н' нагрузки в случае активно-индуктивной нагрузки отстаёт на угол φ_н = arctg (wL_н/R_н) от вектора напряжения на нагрузке U_н'. I_н'= I_н/ n_н; U_н'= U_н n_н. Пренебрегая влиянием анодных индуктивностей, считаем, что обратный выпрямитель потребляет ток, совпадающий по фазе с выходным напряжением. Поэтому вектор I_в1 параллелен U_н1. Ток коммутирующих конденсаторов I_ск1 опережает на 90° вектор U_н1. Векторная сумма токов даёт величину условного вектора входного тока:

I₁₍₁₎= I_н'+ I_в1+ I_ск1 (1.39)

Аналогичные построения можно провести для второго инвертора с учётом того, что вектор U_н2 сдвинут в сторону отставания по отношению к вектору U_н1 на угол ψ. Как видно из векторной диаграммы, величины токов, протекающих в схеме неодинаковы для первого и второго инверторов, и сильно зависят от угла ψ. Это объясняется тем, что если при ψ=0 оба инвертора работают в одинаковых условиях, то при ψ≠0 нагрузка для инверторов оказывается различной. Для 1-го инвертора вектор тока отстаёт от вектора выходного напряжения на угол φ_н+α, т.е. для этого инвертора нагрузка имеет активно-индуктивный характер, причём с увеличением ψ угол φ_н+α также возрастает. Поэтому для работы 1-го инвертора требуется значительная реактивная мощность коммутирующего конденсатора (значительный ток I_ск), которая оказывается избыточной при малых углах ψ. Вследствие этого при значениях ψ близких к нулю токи I_в1 и I₁₍₁₎ сильно возрастают.

Для 2-го инвертора при некоторых значениях ψ≠0 вектор тока I_н' опережает по фазе вектор напряжения U_н2, т.е. для второго инвертора нагрузка имеет активно-ёмкостный характер. Поэтом при ψ≠0 реактивная мощность коммутирующих конденсаторов избыточна, что приводит к увеличению токов I_в2 и I₁₍₂₎. Начиная с некоторого значения ψ, угол опережения вектора тока нагрузки I_н' относительно вектора U_н2 оказывается больше θ. Это означает, что в этом режиме второй инвертор может работать без коммутирующих конденсаторов, т.к. коммутация тока осуществляется за счёт реактивной мощности конденсаторов первого инвертора.

Пользуясь векторной диаграммой можно рассчитать значения токов, протекающих через элементы силовой схемы инверторов. При чисто активной нагрузке (φ_н=0) для 1-го инвертора получаем следующую систему уравнений:

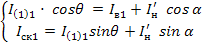_(1.40)

Преобразуем уравнения к виду:

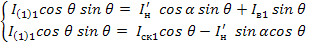(1.41)

Отсюда следует:

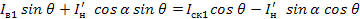(1.42)

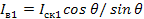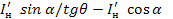- (1.43)

Ток нагрузки при ψ=0 принимаем за номинальный I_н'_ном. Тогда:

I_н' = I_н'_ном cos ψ/2 = I_н'_ном cos α (1.44)

Обозначим: I_в1^* = I_в1/ I_н'_ном; I_ck^* = I_ck/ I_{н ном}

Тогда из (1.43):

I_в1^*= I_ck1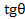^*/ – (0,5 sin 2α/ 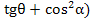(1.45)

Величину необходимого значения тока коммутирующих конденсаторов I_ck1 найдём из следующих соображений. Ёмкость коммутирующих конденсаторов всегда избыточна. За исключением одного случая, когда I_в1=0. При этом из (1.43):

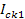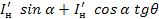= (1.46)

или:

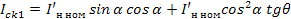(1.47)

Определим значение угла α = ψ/2 при котором необходим наибольший ток I_ck1, дифференцируя уравнение (1.47):

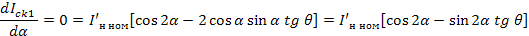
Отсюда:

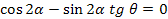
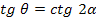
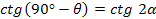
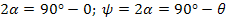(1.48)

Подставляя это значение угла α в выражение для I_ck1^* получим:

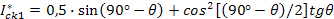(1.49)

Так как: 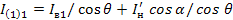, то

I₁₍₁₎^*= I₁₍₁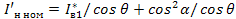₎/ (1.50)

Подставляя в (1.50) значение 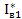выраженное через I_ck1^*, получаем:

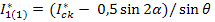(1.51)

Из векторной диаграммы для токов второго инвертора:

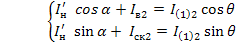(1.52)

Преобразуем уравнение к виду:

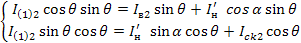(1.53)

Отсюда получаем следующее выражение:

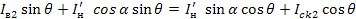(1.53)

Тогда для тока 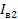можно записать:

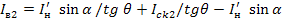(1.54)

Учитывая, что , получаем:

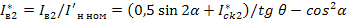(1.55)

Так как с ростом ψ/2=α нагрузка для второго инвертора приобретает всё более ёмкостный характер, то максимально необходимое значение тока 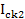имеем при α=0. При этом =0. Отсюда следует, что:

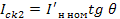(1.56)

С учётом уравнения (1.56) ток 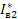можно представить в виде:

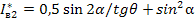(1.57)

Тогда, ток I₍₁₎₂ можно определить из уравнения:

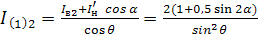(1.58)

Зная значения токов I_в, I₍₁₎, можно рассчитать величины токов, протекающих через вентили инверторов и обратных выпрямителей. Так, средние значения токов вентиля инвертора I_иср и выпрямителя I_вср составляет: I_иср=0,43 I₍₁₎; I_вср=0,43 I_в.

Амплитудные значения токов вентилей при этом равны:

I_{и max} = 1, 28 I₍₁₎; I_{в max} = 1,28 I_в.

Таким образом, давая общую характеристику метода геометрического суммирования можно отметить, что его преимущества заключаются в возможности регулирования:

1) выходного напряжения в широких пределах от 0 до U_{н ном};

2) частоты независимо от выходного напряжения.

Основным недостатком данного метода является существенное увеличение мощности силового оборудования, т.к. по контуру инвертор – обратный выпрямитель циркулируют большие токи, в несколько раз превышающие ток нагрузки.

Метод геометрического суммирования выходных напряжений двух или более инверторных мостов позволяет получить не только регулирование действующего значения выходного напряжения, но и существенно улучшить форму выходного напряжения за счёт исключения ряда нежелательных гармоник. Так в однофазной схеме при m=2 для исключения низкочастотной третьей гармоники можно использовать два инверторных блока с постоянным фазовым сдвигом в ψ₍₃₎=180°/3=60°. Для исключения пятой гармоники необходим фазовый сдвиг ψ₍₅₎= 180°/5=36° и т.д. Таким образом, для исключения n-ой гармоники в выходном напряжении требуется фазовый сдвиг в ψ_(n)= 180°/n.