Анализ АИР методом основной гармоники.

Метод основной гармоники, допускающий использование векторных диаграмм, является удобным для анализа АИР. Предпосылкой его использования служит близкая к синусоиде форма кривой выходного тока инвертора и напряжения на конденсаторе. Поскольку длительности токовых пауз занимают существенно меньшую часть периода выходного тока, то при анализе инвертора этими паузами пренебрегают. Анализ ведется для так называемого граничного режима, временные диаграммы которого представлены на рисунке 2.2.

Выходное напряжение инвертора (напряжение U_и), имеющее

вид двуполярной импульсной кривой, заменяют его первой гармоникой:

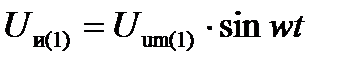, (2.3)

где U_иm(1)=4Е/π – амплитуда первой гармоники;

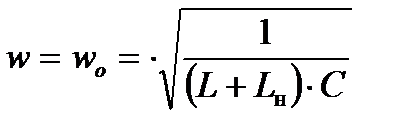- угловая выходная частота.

Действующее значение первой гармоники:

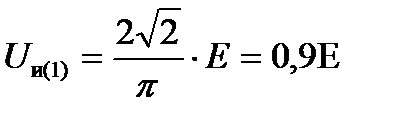(2.4)

Из кривой, рисунок 2.2 г, находим связь среднего значения тока, потребляемого от источника питания, с действующим значением выходного тока инвертора I_и:

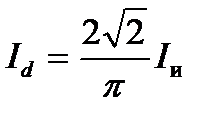(2.5)

Составим уравнение баланса активной мощности:

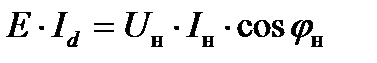(2.6)

После подстановки (2.5) в (2.6) находим связь действующего значения напряжения на нагрузке с действующим значением первой гармоники напряжения инвертора:

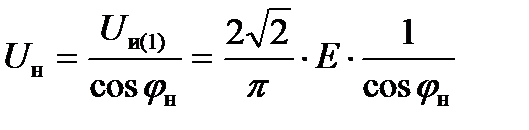(2.7)

Поскольку напряжение инвертора принято синусоидальным, и действующее значение зависит только от величины E, последующий анализ инвертора связан с рассмотрением его эквивалентной схемы замещения (рисунок 2.3) с источником синусоидального напряжения. При расчете элементов L и C, обычно являются заданными напряжение на нагрузке U_н и её параметры R_н и L_н. Построение векторной диаграммы (рисунок 2.4) проводим следующим образом.

Откладываем вектор напряжения U_н на котором, как на диаметре проводим окружность. Под углом к вектору U_н проводим линию направления вектора U_и(1). Точка пересечения с окружностью определяет модуль вектора U_и(1). При w=w_o выходная цепь инвертора оказывается настроенной на резонанс. Это означает равенство суммарного напряжения на индуктивных сопротивлениях напряжению на конденсаторе, находящемуся с ним в противофазе. Для модулей этих напряжений справедливо равенство:

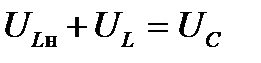(2.8)

От источника U_и(1) потребляется только активная мощность. Ток нагрузки I_H совпадает по фазе с напряжением U_и(1) и активным сопротивлением нагрузки:

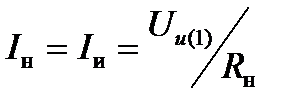(2.9)

Напряжение на нагрузке, помимо (2.7), определяется таким соотношением, получаемым из векторной диаграммы:

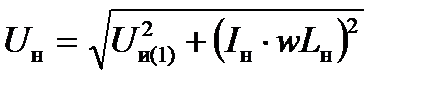(2.10)

Из условия баланса напряжений на реактивных элементах (2.8) находим связь их параметров:

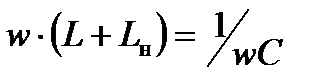(2.11)

или

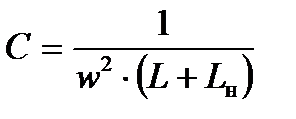(2.12)

При выборе параметров L и C исходят из значений добротности выходной цепи инвертора:

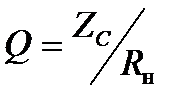(2.13)

где 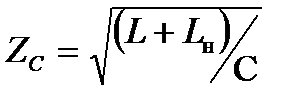- характеристическое сопротивление выходной цепи.

Добротность Q в зависимости от мощности инвертора лежит в пределах 2…5 до 10…12. На основании (2.12) и (2.13) находим выражение для емкости конденсатора C:

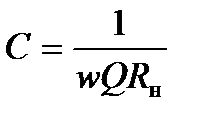(2.14)

Расчет соотношения для величины L получается подстановкой (2.12) в (2.14):

(2.15)