Производная по направлению. Рассмотрим функцию определенную в некоторой окрестности точки и произвольный единичный вектор

Рассмотрим функцию 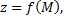определенную в некоторой окрестности точки 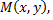и произвольный единичный вектор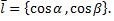

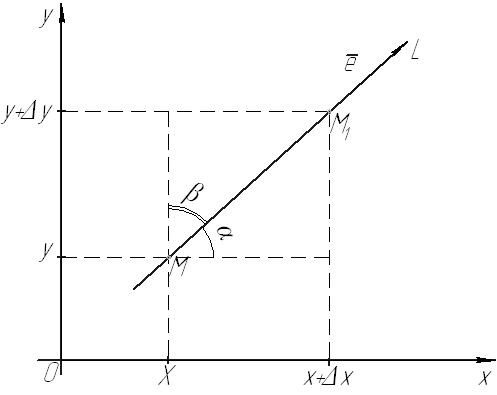
Рис. 34

Производная по направлению

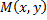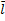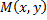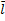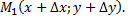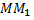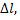Для характеристики скорости изменения функции в точке в направлении вектора введем понятие производной по направлению. Для этого проведем через точку прямую так, чтобы одно из направлений на ней совпадало с направлением вектора , возьмем на направленной прямой точку Обозначим величину отрезка через т.е. 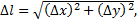если точка 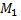расположена так, как показано на рисунке и если точка расположена по другую сторону от точки Функция получит при этом приращение

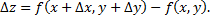
Предел отношения 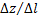при 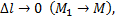если он существует, называется производной функции в точке 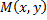по направлению вектора 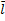и обозначается

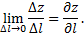
Предположим, что функция 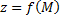дифференцируема в точке Тогда ее приращение вдоль прямой можно записать в виде

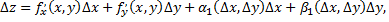
где 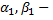бесконечно малые функции при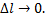

Учитывая, что

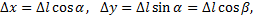
получим

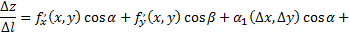
Переходя к пределу в этом равенстве при получаем формулу для производной по направлению

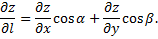
Градиентом функции 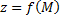в точке 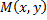называется вектор, координаты которого равны соответствующим частным производным 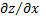и взятым в точке

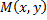
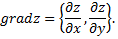
Так как

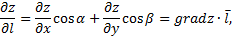
или

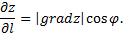
Градиент функции 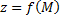в точке 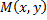характеризует направление и величину максимальной скорости возрастания этой функции в данной точке.

Контрольные вопросы

1. Дать определение функции многих переменных.

2. Что называют областью определения функции многих переменных?

3. Как находят частные производные и дифференциалы первого и высших порядков.

4. Сформулировать теорему о смешанных производных.

5. Что называют градиентом функции?