Логарифмическая производная
При нахождении производных от показательно-степенных функций вида 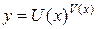 , а также других громоздких функций, допускающих логарифмирование, удобно применить логарифмическую производную.
, а также других громоздких функций, допускающих логарифмирование, удобно применить логарифмическую производную.
Определение: Логарифмической производной от функции y = f(х) называется производная от логарифма этой функции:  . Выведем формулу для вычисления производной показательно-степенной функции
. Выведем формулу для вычисления производной показательно-степенной функции 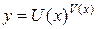 или
или 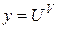 .
.
Прологарифмируем обе части равенства, и воспользуемся свойством логарифма 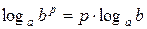 . Получаем:
. Получаем:
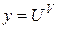 ,
, 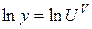 ,
, 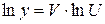 .
.
Продифференцируем обе части равенства и используем правило дифференцирования произведения двух функций:
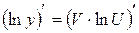 ,
,  ,
, 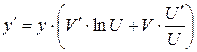 , или окончательно получаем формулу
, или окончательно получаем формулу  , которую можно использовать для вычисления производной показательно-степенной функции вида
, которую можно использовать для вычисления производной показательно-степенной функции вида 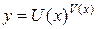 .
.
Пример 1. Вычислить производные данных функций: 1) 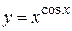 , 2)
, 2) 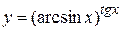 .
.
Решение: 1) 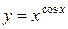 , пусть
, пусть 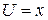 и
и 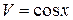 . Тогда
. Тогда 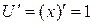 и
и 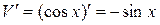 . Подставим эти выражения в полученную формулу
. Подставим эти выражения в полученную формулу
 . Получаем
. Получаем 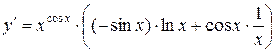 .
.
2) 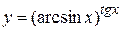 , пусть
, пусть 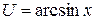 и
и 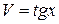 , тогда
, тогда 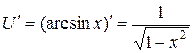 и
и 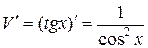 . Получаем
. Получаем 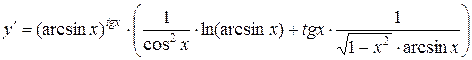 =
= 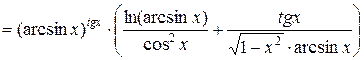 .
.
Дата добавления: 2015-08-21; просмотров: 2295;
