Производная сложной функции. Пусть переменная у есть функция от переменной j, т.е
Пусть переменная у есть функция от переменной j, т.е. а переменная j в свою очередь есть функция от независимой переменной х, т.е. j = j(х). Тогда говорят, что задана сложная функция у = f(j(x)).
Теорема: Если y = f(j) и j = j(х) дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е.
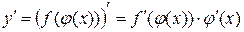 .
.
Правило дифференцирования сложной функции может быть записано и в других формах: 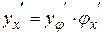 или
или  .
.
Используя формулы для дифференцирования элементарных функций и правило дифференцирования сложной функции, можно составить ещё одну таблицу производных с учетом сложности функций. Пусть 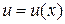 , тогда получаем:
, тогда получаем:
| Название функции | Производная функции |
| Степенная | 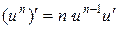 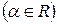 ; ;
|
| Показательная | 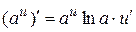 ; ; 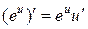 ; ;
|
| Логарифмическая |  ; ;  ; ;
|
| Тригонометрические | 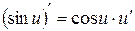 ; ;  ; ;
 ; ; 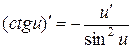 ; ;
|
| Обратные тригонометрические | 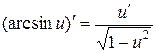 ; ;  ; ;
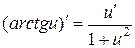 ; ; 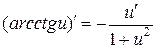 . .
|
Пример 3. Найти производную функции:
1) 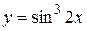 , 2)
, 2) 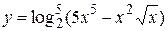 , 3)
, 3) 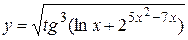 .
.
Решение: 1) 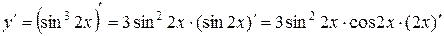 =
=
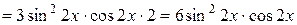 .
.
2)  =
=
= 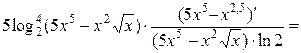
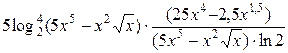 .
.
3) 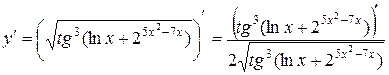 =
=
= 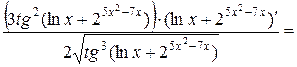
= 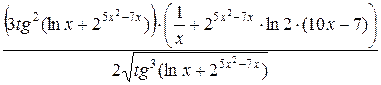 .
.
Дата добавления: 2015-08-21; просмотров: 1021;
