Схема вычисления производной
Производная функции y = f(x) может быть найдена по следующей схеме:
1) Дадим аргументу х приращение Dх ¹ 0 , х + Dх.
2) Найдем значение функции f(x + Dх).
3) Находим приращение функции Dу = f(x + Dх) - f(x).
4) Составляем отношение 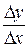 .
.
5) Находим предел этого отношения при Dх ® 0, т.е. 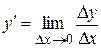 (если этот предел существует).
(если этот предел существует).
Пример 1. Найти производную функции у = х3, используя определение.
Решение:
1) х+Dх, 2) f(x + Dх) = (x + Dх)3 = х3 + 3х2Dх + 3хDх2 + Dх3;
3) Dу = f(x + Dх) - f(x) = х3 + 3х2Dх + 3хDх2 + Dх3 - Dх3 = 3х2Dх + 3хDх2 + Dх3.
4) 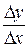 = 3х2 + 3хDх + Dх2.
= 3х2 + 3хDх + Dх2.
5) 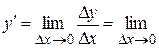 (3х2 + 3хDх + Dх2) =
(3х2 + 3хDх + Dх2) = 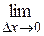 3х2 +
3х2 + 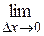 3хDх +
3хDх + 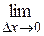 Dх2 = 3х2 +0 +0 = 3х2.
Dх2 = 3х2 +0 +0 = 3х2.
Можно доказать, что для любого (не только натурального) n имеем формулу производной степенной функции - 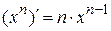 . Полезно знать частные случаи этой формулы при n =
. Полезно знать частные случаи этой формулы при n =  и n = -1.
и n = -1.
 ;
; 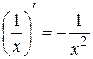 .
.
Используя определение производной функции можно вывести формулы для дифференцирования основных элементарных функций. Ниже приведены некоторые элементарные функции и их производные.
| Название функции | Алгебраическая формула | Производная функции |
| Степенная | 
| 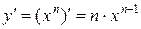
|
| Показательная | 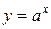
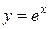
| 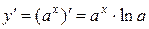
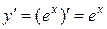
|
| Логарифмическая | 
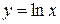
| 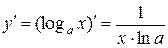
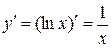
|
| Тригонометрические | 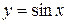
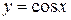
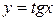
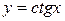
| 
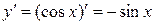
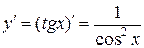
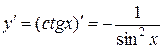
|
| Обратные тригонометрические |
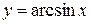

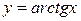

| 
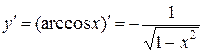

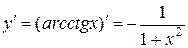
|
Дата добавления: 2015-08-21; просмотров: 2570;
