Задачи, приводящие к понятию производной

Лекция 1. Понятие производной. Основные правила

Дифференцирования

Задачи, приводящие к понятию производной

1.1 Задача о касательной

Пусть на плоскости Oxy дана непрерывная кривая y = f(x) и необходимо найти уравнение касательной к этой кривой в точке M₀(x₀;y₀).

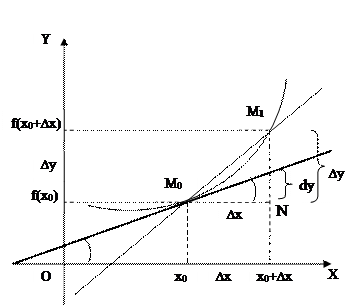
Пусть M₀M₁ – секущая , 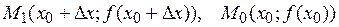. Под касательной к кривой y = f(x) в точке M₀ естественно понимать предельное положение секущей M₀M₁ при приближении точки M₁ к точке M₀, т.е. при Dх®0.

Уравнение прямой, проходящей через точку M₀, в соответствии с формулой уравнения прямой, проходящей через точку M₀:

, .

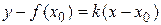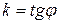Из DM₀M₁N имеем при приближении точки M₁ к точке M₀, что 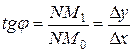. Значит угловой коэффициент касательной .

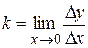Таким образом, уравнение касательной можно записать так:

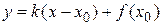, где .

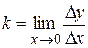1.2 Задача о скорости движения

Пусть вдоль некоторой оси движения точка по закону S = S(t), где S – пройденный путь, t – время, и необходимо найти скорость точки в момент t₀.

К моменту времени t₀ пройденный путь равен S₀= S(t₀), а к моменту (t₀+t) - путь S₀+DS = S(t₀+t).

Тогда за промежуток Dt средняя скорость будет 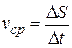. Чем меньше Dt, тем лучше средняя скорость характеризует движение точки в момент t₀. Поэтому под скоростью точки в момент t₀ естественно понимать предел средней скорости за промежуток от t₀ до t₀+Dt, тогда Dt®0, т.е.

.

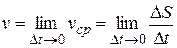3.1 Задача о производительности труда

Пусть функция U = U(t) выражает количество произведенной продукции U за время t и необходимо найти производительность труда в момент t₀.

За период времени от t₀ до t₀+Dt количество произведенной продукции изменяется от значения U₀ = U(t₀) до значения U₀+DU = U(t₀+Dt); тогда средняя производительность труда за этот период времени 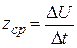. Очевидно, что производительность труда в момент времени t₀ можно определить как предельное значение средней производительности за период времени от t₀ до t₀+Dt при Dt®0, т.е.

.

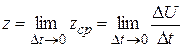Рассматривая три различные по характеру задачи, мы пришли к пределу одного вида. Этот предел играет очень важную роль в математическом анализе, являясь основным понятием дифференциального исчисления.