Глава 1. Определение производной. Правила дифференцирования.
Пусть задана некоторая функция y = f (x). Выберем в области определения функции два произвольных значения аргумента х их1. Вычислим значения функции f(x) и f(x1). Обозначим за Dх разность между двумя значениями аргумента Dх = х1 – х, (т.е х1 = х +Dх).
Замечание. Dхможет быть как больше нуля, если х1 > х,так именьше нуля, если х1 < х.
Приращением функции Df (x) называется разность между двумя соответствующими значениями функции Df(x) = f(x1) - f(x) или Df(x) = f(х + Dx) – f(x).
Если при Dх® 0 существует конечный предел отношения приращения функции к вызвавшему его приращению аргумента, то функция f(x) называется дифференцируемой в точкех, а значение предела называется производной от функцииf(x) в точке х и обозначается
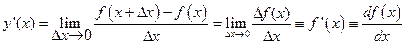
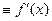 (1.1)
(1.1)
Производная - это функция от того же аргумента, что и f(x). Операцию вычисления производной называется дифференцированием функции.
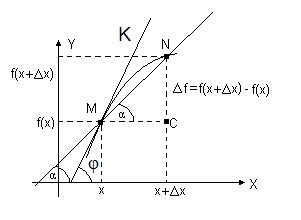
Геометрический смысл производной. Если изобразить на рисунке график функции f(x), отметить точки х и х1 = х + Dх , то МС = Dх, NC = Df(x). Величина отношения
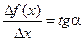 (1.2)
(1.2)
равна тангенсу угла наклона секущей MN к оси абсцисс (см. рис.1.1).
|
Если Dх ® 0, то точка N стремится по графику функции к точке M, секущая MN стремится занять положение касательной МК к графику функции f(x) в точке M, угол наклона секущей α стремится к углу наклона касательной φ. Сравнивая формулы (1.1) и (1.2) мы можем сказать, что значение производной f ¢(x) в точке х равно тангенсу угла наклона касательной к графику y = f(x) в точке М с координатами (х, f(x)).
Уравнение касательной в точке М
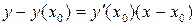 ,
,
уравнение нормали
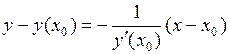 ,
,
В механике производная от пути по времени есть скорость
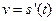
Дата добавления: 2015-08-26; просмотров: 1043;
