Основные правила дифференцирования
1. Производная постоянной величины равна нулю, т.е. 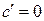 .
.
2. Производная аргумента равна 1, т.е. 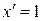 .
.
Пусть u = u(x) и v = v(x) дифференцируемые функции, тогда:
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т. е. 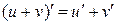 .
.
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.
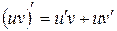 .
.
Следствие 1. Постоянный множитель можно выносить за знак производной: 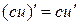 .
.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений каждого из сомножителей на все остальные
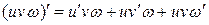 .
.
5. Производная частного двух дифференцируемых функций может быть найдена по формуле
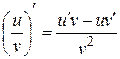 ,
, 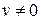
Пример 1. Найти производную функции y = f(x) и вычислить ее значение в точке х = 1:
а) 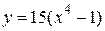 ; б)
; б) 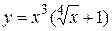 ; в)
; в) 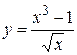 .
.
Решение: а) 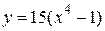 ,
,
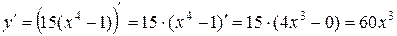 .
.
б) 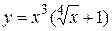 , применим правило дифференцирования произведения двух функций и формулы для степенных функций
, применим правило дифференцирования произведения двух функций и формулы для степенных функций 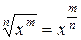 и
и 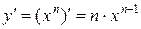 . Получаем:
. Получаем:
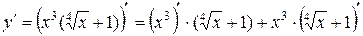 =
= 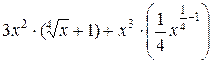 = =
= = 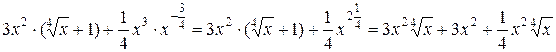 = =
= = 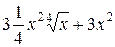 .
.
в) 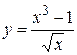 , применим правило дифференцирования частного двух функций и формулы для степенных функций
, применим правило дифференцирования частного двух функций и формулы для степенных функций 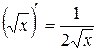 и
и 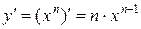 . Получаем:
. Получаем:
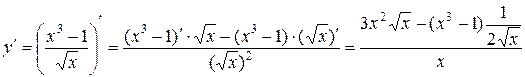 =
=
= 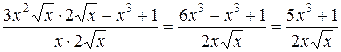 .
.
Пример 2. Составить уравнение касательной к кривой 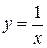 в точке х = 1.
в точке х = 1.
Решение: используя геометрический смысл касательной, запишем уравнение касательной в виде: 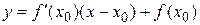 . Для этого найдем производную функции и её значение в точке х0 = 1.
. Для этого найдем производную функции и её значение в точке х0 = 1.
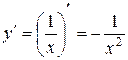 ,
,  . А также необходимо найти
. А также необходимо найти  . Найденные значения подставляем в формулу:
. Найденные значения подставляем в формулу: 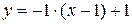 , или
, или 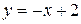 .
.
Ответ: уравнение касательной к графику функции 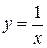 в точке
в точке 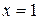 имеет вид
имеет вид 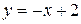 .
.
Дата добавления: 2015-08-21; просмотров: 1089;
