Определение производной
Определение 2.1Пусть функция y = f(x) определена в некоторой окрестности точки х0. Предел отношения приращения Dу функции в этой точке (если он существует) к приращению Dх аргумента, когда Dх ® 0, называется производной функции f(x) в точке х0.
Обозначения: 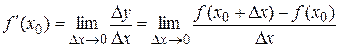 или
или
 .
.
Вычисление производной называется дифференцированием функции.
Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой очке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
Из задачи о касательной вытекает геометрический смысл производной: производная 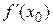 есть угловой коэффициент касательной (тангенс угла наклона), проведенной к кривой y = f(x) в точке х0, т.е.
есть угловой коэффициент касательной (тангенс угла наклона), проведенной к кривой y = f(x) в точке х0, т.е.  .
.
Тогда уравнение касательной к кривой y = f(x) в точке M(х0, f(x0)) примет вид
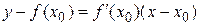 или
или 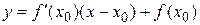 .
.
Уравнение нормали (перпендикуляра) к кривой y = f(x) в точке M(х0, f(x0)) имеет вид:
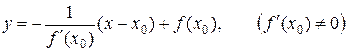 .
.
Из задачи о скорости движения следует механический смысл производной: производная пути по времени  есть скорость точки в момент
есть скорость точки в момент 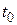 :
:  , а производная скорости по времени
, а производная скорости по времени 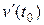 есть ускорение точки в момент
есть ускорение точки в момент 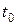 :
:  .
.
Из задачи о производительности труда следует, что производная объема произведенной продукции по времени 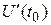 есть производительность труда в момент
есть производительность труда в момент 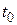 .
.
Дата добавления: 2015-08-21; просмотров: 1290;
