Геометрический смысл производной и дифференциала
Пусть на плоскости с д.п.с.к. X0Y определена и дифференцируема функция y=f(x) в некоторой области т. 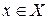 .
.
1. Тогда приращение функции 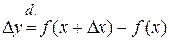 .
.
2. Приращение касательной 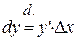 .
.
Действительно, пусть две точки M и N принадлежат кривой L.
| Def.1 | Секущей называют прямую, проходящую через любые две точки кривой. |
| Def.2 | Касательной к кривой L в т. M называют предельное положение секущей при N→M. |

Пусть кривая L в д.п.с.к. X0Y задана явно y=f(x).
Тогда из прямоугольного 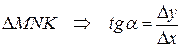 , если т. N → т. M, то
, если т. N → т. M, то  , или угловой коэффициент касательной
, или угловой коэффициент касательной
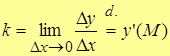 .
.
Пусть т. M0 (x0, y0)  L, тогда уравнение прямой, проходящей через т. М0 с заданным угловым коэффициентом k , имеет вид
L, тогда уравнение прямой, проходящей через т. М0 с заданным угловым коэффициентом k , имеет вид
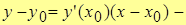 уравнение касательной.
уравнение касательной.
Пусть нормаль – прямая, проходящая через т. М0 перпендикулярно касательной, тогда
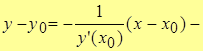 уравнение нормали.
уравнение нормали.
| Note ! | Дифференциал геометрически равен приращению касательной, в отличие от приращения функции. |

| Note ! | Следует заметить, что (в зависимости от выпуклости или вогнутости графика функции y=f(x)) дифференциал dy может быть как меньше, так и больше приращения функции. Однако в любом случае дифференциал – главная, линейная его часть. |
Дата добавления: 2015-08-20; просмотров: 1204;
