А — объект управления; б — релейно-контактная схема; в — минимизированная схема
В случае тонкого и узкого пиломатериала значения этих сигналов будут х1 = 0 и х2 = 0; при толстом и широком — х1 = 1, х2= 1. Но комбинация значений входных сигналов 0 0 будет и в случае, когда пиломатериала не будет на роликовом конвейере; поэтому необходимо ввести еще датчик х3, фиксирующий наличие пиломатериалов на рольганге.
3. Составить таблицу состояний (табл. 6).
ТАБЛИЦА СОСТОЯНИЙ
| Номера КОвходныЦхИ?игнаалоНвИЙ Значения вых°«ных сигяалов комбинаций *1 *2 *3 У, У* УЗ У4. 00000000 10 0 1 10 0 0 2 0 10 0 0 0 0 3 0 1 10 10 0 4 10 0 0 0 0 0 5 10 10 0 10 "6 1 10 0 0 0 0 7 1110 0 0 1 |
4 Получение логических функций. Логических функций будет четыре, по числу выходных сигналов. Каждая функция получается путем перемножения переменных х1, х2 и х3, описанных с тех строк таблицы, где данная функция равна 1. Переменная записывается соответственно с отрицанием или без отрицания, если входной сигнал равен 0 или 1.
Логические функции, описывающие систему управления индикатором, будут следующие:
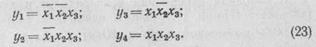
5 Построить варианты исходной схемы системы управления (рис. 79, б). В схеме у1 у2, у3 и y4—лампы индикатора, соответствующие одному из сечений пиломатериала, а х1, х2 и х3 контакты конечных выключателей. Из схемы видно, что, например, лампа у2 загорится при воздействии на выключатели х2 и х3, то есть при тонком и широком пиломатериале.
6. Минимизация логических функций. Каждая логическая функция системы уравнений (23) сразу получается в минимальной форме. Но так как в каждую функцию входят одни и те же переменные x1 x2 и х3, то минимизация возможна, если функции (23) записать в виде одной многовыходной функции Ф
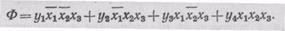
Используя сочетательный закон, запишем функцию Ф в виде
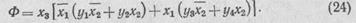
7. Построение схемы минимизированной функции (24).
На рис. 79, в показана эта схема. Сравнение схем (рис. 79, б и б) показывает, что минимизированная схема содержит на пять контактов меньше, чем исходная.
S 40. СИНТЕЗ МНОГОТАКТНЫХ СИСТЕМ ЛОГИЧЕСКОГО УПРАВЛЕНИЯ
В отличие от однотактных систем управления, одинаково реагирующих на один и тот же сигнал или совокупность сигналов на входе, многотактные системы управления на одну и ту же ситуацию на входе могут реагировать по-разному. Значение выходной переменной многотактной системы управления зависит от предшествующих ситуаций на входе, т. е. от последовательности изменения значений входных переменных.
Работу элементов многотактных систем управления удобно изображать циклограммой. Для составления математической модели многотактных систем управления необходимо определить условия включения и выключения исполнительных механизмов.
В отличие от однотактных систем управления, где условиями включения и выключения являются комбинации значений вход-
ных переменных, в многотактных системах управления условиями включения и выключения являются те значения входных переменных, переход в которые вызывает изменение состояния выходной переменной.
Условия включения и выключения. Условием включения f' выходной переменной является такое значение входной переменной, при переходе в которое выходная переменная переходит в единичное состояние:
а) выходная переменная у1 переходит в единичное состояние (включается) при переходе в единичное состояние (включение) входной переменной х1 (рис. 80, a): f'y1= x1;
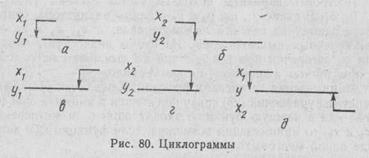
б) выходная переменная у2 переходит в единичное состояние (включается) при переходе в нулевое состояние (выключение) входной переменной х2 (рис. 80, б): fy2 = 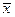 2.
2.
Условием выключения f" для выходной переменной является такое значение входной переменной, при переходе в которое выходная переменная переходит в нулевое состояние:
а) выходная переменная у1 переходит в нулевое состояние (вы
ключается) при переходе в единичное состояние (включение) вход
ной переменной х1 (рис. 80, в): f’’y1=x1;
б) выходная переменная у2 переходит в нулевое состояние (вы
ключается) при переходе в нулевое состояние (выключение) вход
ной переменной х2 (рис. 80, г): f’’y2= 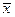 2.
2.
Основное условие работы исполнительного механизма — наличие на входе системы управления условий включения и отсутствие условий выключения для данного элемента: у = f'y 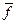 ''y.
''y.
Для многотактных систем управления это условие является необходимым, но недостаточным. Недостаточность проявляется тогда, когда при одних и тех же значениях входных переменных выходная переменная имеет различные значения.
Рассмотрим систему управления, заданную следующей циклограммой (рис. 80, д). Данная система при отсутствии сигналов на входе х1 = 0 и х2 = 0 должна иметь переменную у в нулевом состоянии на выходе в одном случае, в единичном состоянии — в другом.
Как видно из данной циклограммы, значение выходной переменной у зависит только от последовательности появления сигналов на входе. Если на входе системы управления появляется сигнал х1, соответствующий условиями включения переменной, то данная переменная должна перейти в единичное состояние и сохранять его сколь угодно долго при выключении сигнала х1.
При появлении на входе сигнала х2, соответствующего условиям выключения переменной у, данная переменная должна перейти из единичного состояния в нулевое и сохранять это состояние при выключении сигнала х2.
Для реализации данного закона управления необходимо, чтобы система управления могла сохранять (помнить) сигналы, поступающие на вход систем управления и при необходимости управлять
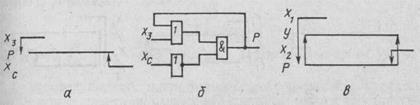
Рис. 81. Элемент «Память»: а — циклограмма; б — элемент «Память»; в — циклограмма
исполнительными механизмами при последующем изменении данных входных переменных.
Эту функцию в многотактных системах управления выполняет элемент «Память» — трехполюсник (два входа и один выход), имеющий два устойчивых состояния. Элемент «Память» способен включаться (Р = 1) при поступлении на вход «Запись» сигнала х3 и оставаться в этом состоянии, пока не поступит сигнал на вход «Стирание» хс.
Работа данного элемента изображается циклограммой, представленной на рис. 81, а, математическая модель его следующая:
Р = (х3 + Р) 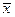 с.
с.
Эта модель может быть реализована на бесконтактных логических элементах (рис. 81, б).
Присутствие элемента «Память» в системах управления является дополнительным условием на включение или выключение исполнительных механизмов. В данном примере условием включения
является хх, т. е. fy = xx.
При отсутствии этого сигнала на входе условия включения для элемента у создаются дополнительным элементом «Память»
f'y= х1 + P.
Элемент память должен включаться при появлении сигнала хх и сохранять единичное состояние выходной переменной у до появления сигнала x2 т. е. х3 = х1 и хс = х2.
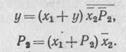
|
| Математической моделью системы управления будет следующая система логических выражений: |
Условие выключения переменной у запоминать не надо, так как она в периоде включения переменной у своего значения не меняет:
f’’y=x2
В целом математическая модель процесса будет следующая:
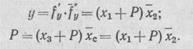
Работа элемента «Память» на циклограмме системы управления изображена на рис. 81, в. Исходя из этой циклограммы, можно заключить, что у = Р. Следовательно, систему управления можно упростить, заменив элемент «Память» на обратную связь или самоблокировку.
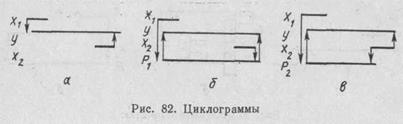
Рассмотрим еще один характерный случай применения элемента «Память». В качестве примера возьмем систему управления, которая задана циклограммой, приведенной на рис. 82, а. Из циклограммы видно, что включение сигнала хх является условием включения функции у: f’y = x1.
Выключение сигнала х2 является условием выключения функции у: f"y = 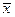 2.
2.
Теперь необходимо рассмотреть условия включения и выключения на достаточность. Условия включения f'y = x1 являются недостаточными, так как сигнал х1 выключается, а функция у должна сохранять единичное состояние. Следовательно, условия включения должны быть дополнены элементом «Память» f'y = x1 + P1 (рис. 82, б). Поскольку у = Р1 элемент «Память» должен быть заменен самоблокировкой f'y = x1+y.
Условия выключения f"y = 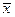 2 также являются недостаточными, так как сигнал х2 находится в нулевом состоянии и тот период времени, где функция у должна быть включена.
2 также являются недостаточными, так как сигнал х2 находится в нулевом состоянии и тот период времени, где функция у должна быть включена.
Сохранять единичное состояние функции у будет дополнительный элемент «Память» Р2. Элемент «Память» должен быть включен в тот период времени, когда должна быть включена функция у, но имеются условия выключения х2 (рис. 82, в).
Функция у должна выключаться, когда созданы условия выключения и не включена память Р2, т. e. f"y = 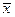 2
2 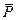 2.
2.
Для элемента «Память» Р2 в данном случае х3 = х1 и хс = х2.
Из вышеизложенного можно сделать вывод, что для синтеза многотактной системы управления необходимо:
1) определить необходимые и достаточные условия включения (f'yi выходных переменных у1; 2) определить необходимые и достаточные условия выключения f''yi выходных переменных yi ; 3) синтезировать математическую модель системы управления по логическому выражению
где yi= f'yi 
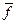 ''yi — число
''yi — число  выходных переменных системы управления.
выходных переменных системы управления.
В простых случаях математическую модель системы управления можно составить по словесному описанию работы объекта управления. При этом необходимо определить условия включения и выключения, очередность и продолжительность их действия. Затем по словесному описанию или циклограмме составляют логические уравнения математической модели. Далее проводят анализ полученных уравнений с точки зрения минимизации элементов и, наконец, составляют принципиальную схему управляющего устройства технологическим объектом. Проиллюстрируем эту очередность и условия составления схемы управляющего устройства.
Синтез многотактной системы управления.Требуется синтезировать схему управляющего устройства для опускания и подъема прижимной линейки (утюжка) шлифовального станка.
1. Описание условий работы объекта управления (рис. 83, а).
По роликовому конвейеру 1 перемещается мебельный щит 2. В по
ложении щита I, когда его передняя кромка окажется в зоне ин
струмента, прижимная линейка 3 с помощью пневмоцилиндра 4
прижимает движущуюся шлифовальную ленту 5 к поверхности
щита 2. В положении II, когда задняя кромка его выходит из
зоны инструмента, прижимная линейка 3 отводит ленту 5 от
обрабатываемой поверхности.
2. Установить число входных и выходных переменных. В слу
чае применения пневмоцилиндра одностороннего действия (обрат
ный ход поршня происходит за счет пружины) выходной сигнал
будет один — у — команда на перемещение поршня вниз.
Для фиксации положения щитов на роликовом конвейере необходимо установить датчики положения х1 и х2. Место расположения датчиков может быть различным. Рассмотрим вариант, когда при съезде щита с датчика х1 линейка опускается, а при наезде надатчик х2 — поднимается.
3. Построение циклограммы работы управляющего устройства. За один цикл работы объекта управления или управляющего устройства примем время обработки одного щита. Так как за это время прижимная линейка опустится один раз, то на циклограмме
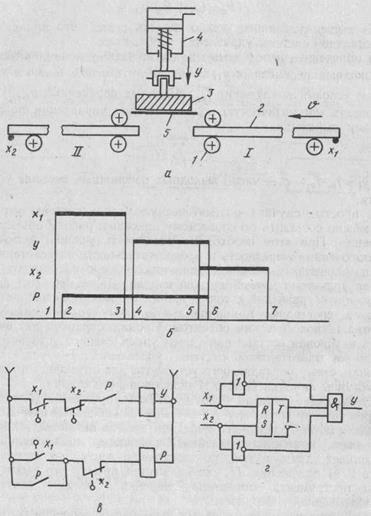
Рис. 83. Система логического управления:
а - объект управления; б - циклограмма; в - релийно-контактная схема- г - схема
управления на бесконтактных элементах
(рис. 83, б) будет иметь место только один период включения элемента у (интервал 4—5).
4. Математическая модель системы управления, прижимной линейкой шлифовального станка. Во включающем такте 3—4 сиг-
нал х1 исчезает, следовательно, условие срабатывания элемента у запишется формулой f’y = 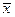 1. В отличающем такте 5—6 сигнал х2 появляется, поэтому условие выключения будет f’’y — x2.
1. В отличающем такте 5—6 сигнал х2 появляется, поэтому условие выключения будет f’’y — x2.
Первоначальный вид логической функции запишется как
В течение включающего 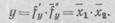 периода у (интервал 3—5) нет ни сигнала х1, ни сигнала х2. Но такое же сочетание сигналов х1 и х2 имеет место на циклограмме и в интервале 7—1. Следовательно, здесь элемент у тоже будет включен, а это противоречит условию работы. Необходимо запретить срабатывание элемента у в интервале 7—1. Этого достигают введением в управляющее устройство элемента «Память» — Р.
периода у (интервал 3—5) нет ни сигнала х1, ни сигнала х2. Но такое же сочетание сигналов х1 и х2 имеет место на циклограмме и в интервале 7—1. Следовательно, здесь элемент у тоже будет включен, а это противоречит условию работы. Необходимо запретить срабатывание элемента у в интервале 7—1. Этого достигают введением в управляющее устройство элемента «Память» — Р.
На циклограмме (рис. 83, б) сигнал Р должен иметь различное значение в интервалах 3—5 и 7—1, где Х1 и Х2 равны 0. Это условие будет выполнено, если в интервале 1—5 сигнал Р будет равен 1, то есть сигнал Р появится при появлении х1 и исчезнет при появлении х2.
После введения переменной Р функция у выхода примет вид
у= 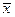 1
1 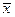 2Р. (25)
2Р. (25)
Аналогично выполняется математическое описание функционирования введенного элемента памяти Р. Условия включения и выключения для элемента Р будут соответственно f'P = x1
и f"P = х2.
Первоначальный вид функции Р запишется как
Р = x1 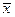 2. (26)
2. (26)
Из этого выражения можно видеть, что элемент Р будет включен только в интервале 2—3, а далее отключится, так как сигнал х1 исчезнет. Чтобы обеспечить работу во всем периоде включения (интервал 2—6), следует ввести элемент памяти. В данном случае роль элемента памяти может выполнять сам элемент Р.
Переменная Р вводится в функцию (26) через операцию логического сложения с переменной х1. Тогда окончательно функция (26) запишется как
Р = (х1 + Р) 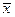 2. (27)
2. (27)
Логические функции (25), (27) и представляют собой математическую модель системы логического управления прижимной линейкой шлифовального станка.
5. Составление варианта схемы, выполненной на релейно-кон-
тактных элементах. На рис. 83, в показан вариант схемы управ
ляющего устройства, выполненной на релейно-контактных эле
ментах. В этой схеме замыкание контактов электромагнитного реле
у подает команду на перемещение поршня пневмоцилиндра при
жима линейки.
6. Составление варианта схемы управляющего устройства на
бесконтактных элементах. В многотактных управляющих устройст-
вах память реализуется с помощью триггера, а комбинационная часть схемы — на логических элементах. Схема управляющего устройства (рис. 83, г) для управления шлифовальным станком выполнена с применением RS-триггера с раздельными входами.
Дата добавления: 2015-07-14; просмотров: 3921;
