ОСНОВНЫЕ ФОРМАЛИЗОВАННЫЕ ЯЗЫКИ ОПИСАНИЯ ЛОГИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ
Для описания работы объекта управления можно использовать различные формализованные языки. Описать работу объекта управления в соответствии с технологическим процессом — это значит задать определенный порядок переходов из одних внутренних состояний в другие при воздействии соответствующих комбинаций входных сигналов.
К формализованным языкам, используемым при описании логических систем управления, относятся математический аппарат алгебры логики, таблицы состояний, циклограммы и др.
Преобразования алгебры логики.Математическим аппаратом для описания работы логических устройств служит двузначная алгебра логики, которая изучает связи между переменными, принимающими только два значения. Этим двум значениям ставятся в соответствие различные взаимоисключающие действия, условия или состояния: замыкание контакта (1) — размыкание контакта (0); наличие сигнала (1) — отсутствие сигнала (0); движение рабочего органа (1) — неподвижное состояние рабочего органа (0).
Логической переменной называется величина, способная принимать только два значения —- 0 или 1, обычно переменные обозначаются буквами латинского алфавита.
Логической функцией называется зависимость выходных переменных от входных. Она также может принимать только два значения — 0 или 1.
Различные комбинации входных переменных называются наборами. Функция является полностью заданной, если указаны ее значения для всех наборов входных переменных.
Число наборов переменных определяют по формуле N = 2n, где п — число переменных.
Если все п состояния xi входных переменных системы управления занести в строки таблицы и для каждого состояния определить значение логической функции, то такая таблица будет называться таблицей состояний системы логического управления. Таблица состояний является моделью системы управления и полностью определяет логическую функцию.
В общем виде логическая функция может быть описана выражением y = F (х1, х2, . . ., хп), которое читается как: у есть функция логических переменных х1 . . . хп.
В математической логике рассматриваются несколько основных логических связок между переменными: логическое умножение (функция И), логическое сложение (функция ИЛИ), логическое
отрицание (функция НЕ), импликация, равнозначность, универсальные функции Шеффера и Пирса и др. Любое логическое устройство можно построить, используя три главные связки (функции): И, ИЛИ и НЕ. Все остальные являются производными от этих основных функций.
Для иллюстрации связи между логическими уравнениями и реальными схемами воспользуемся реальными релейно-контакт-ными схемами и бесконтактными элементами. Истинному значению переменной (1) соответствуют нормально разомкнутые контакты, ложному значению переменной (0) нормально замкнутые контакты.
Функция И. Логическое уравнение у — х1  х2 читается так: у истинно, если истинны х1 и х2 (рис. 73, а).
х2 читается так: у истинно, если истинны х1 и х2 (рис. 73, а).
При описании функционирования объектов автоматизации и проектирования логических систем управления необходимо стремиться к логическим уравнениям, имеющим минимальное число элементов (переменных).
Существуют определенные правила, которые позволяют преобразовывать логические уравнения без изменения их действия.
Рассмотрим основные преобразования алгебры логики.
1. Логическое произведение любого числа переменных обращается в нуль, если одна из переменных имеет значение 0 (постоянно разомкнутой элемент), независимо от значений других переменных
0  x1
x1  x2
x2  x3 . . .xn= 0.
x3 . . .xn= 0.

Рис. 73. Логический элемент И:
а — таблица состояний; б — релейно-контактная схемагв — условное обозначение бесконтактного элемента И
Рис. 74. Логический элемент ИЛИ:
а —. таблица состояний; б — релейно-контактная схема; в — условное обозначение
Логическому умножению соответствуют последовательно соединенные контакты (рис. 73, б). Контакты включены в цепь катушки электромагнитного реле Р, нормально разомкнутые контакты которого являются выходом схемы.
На рис. 73, а, в показаны таблица состояния для функции И
и изображение бесконтактного логического элемента И на два входа.
Функция ИЛИ. Логическое уравнение у = х1 + х2 читается следующим образом: у истинно, если истинны х1 или х2 или оба одновременно.
Операции логического сложения соответствует параллельное соединение контактов (рис. 74, б). Эти контакты включены в цепь электромагнитного реле Р, нормально разомкнутые контакты А которого являются выходом схемы.
На рис. 74, а, в показаны таблица состояний для функции ИЛИ и изображение бесконтактного логического элемента на два входа.
Функция НЕ. Логическое уравнение у = 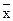 1 читается следующим образом: у истинно, когда х1 ложно, и наоборот.
1 читается следующим образом: у истинно, когда х1 ложно, и наоборот.
Логическому отрицанию соответствует нормально замкнутый контакт (рис. 75, а). Этот контакт включен в цепь катушки электромагнитного реле Р, нормально замкнутый контакт которого является выходом этой схемы.
На рис. 75, б, в показаны таблица состояний для функции НЕ и изображение бесконтактного логического элемента НЕ.

2. Логическая сумма любого числа переменных обращается
в единицу, если одна из переменных имеет значение 1 (постоянно
замкнутый элемент), независимо от значений других переменных
1+х1+х2+х3+ . . . +хп=1.
3. Логическая сумма любой логической переменной и перемен
ной, имеющей значение 0, равна той же логической переменной
х + 0 = х.
4. Логическое произведение любой логической переменной и пе
ременной, имеющей значение 1, равно той же логической перемен
ной
х  1 = х.
1 = х.
5. Логическое произведение или логическая сумма нескольких
одинаковых переменных равны одной и той же переменной
x1  x1
x1  x1
x1  x1 . . . x1=x1;
x1 . . . x1=x1;
x1 + x1 + x1 + x1 . . .+x1=x1.
6. Логическое произведение любой переменной и ее инверсии
есть 0
х 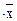 =0.
=0.
7. Логическая сумма любой переменной и ее инверсии есть 1
х+ 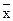 =1.
=1.
8. Логическая переменная с двойной инверсией равна данной
логической переменной
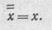
9. Закон перемещения:
x1  x2 = x2
x2 = x2  x1 ; x1 + x2 = x2 + x1.
x1 ; x1 + x2 = x2 + x1.
10. Закон сочетания:
x1  (x2
(x2  x3.)=( x1
x3.)=( x1  x2)
x2)  x3; x1 + (x2 + x3.)=( x1 + x2) + x3
x3; x1 + (x2 + x3.)=( x1 + x2) + x3
11. Закон распределения:
x1  x2+ x1
x2+ x1  x3= x1
x3= x1  (x2 + x3.).
(x2 + x3.).
12. Закон поглощения:
x1  (x1 + x2.)= x1; x1+
(x1 + x2.)= x1; x1+ 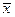 1
1  x2=x1 + x2;
x2=x1 + x2;
x1+ x1  x2+ x1
x2+ x1  x3+ …+ x1
x3+ …+ x1  xn.= x1.
xn.= x1.

Рис. 76. Логический элемент ИЛИ—НЕ:
a —_ таблица состояний; б — релейно-контактная схема; в — условное обозначение; г, д, е — реализация основных логических функций на элементах ИЛИ—НЕ
13. Закон инверсии:
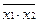 =
= 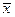 1+
1+ 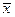 2;
2;  =
= 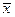 1
1 
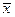 2.
2.
Применяют и другие, более сложные, законы преобразования логических уравнений.
Помимо основных логических функций И, ИЛИ и НЕ существует ряд более сложных логических функций. Наибольшее распространение при синтезе систем логического управления получили две универсальные логические функции, каждая из которых позволяет реализовать основные логические функции И, ИЛИ и НЕ, а значит, и реализовать на этих элементах систему логического управления любой сложности. Это функции ИЛИ — НЕ (функция «стрелка Пирса») и И — НЕ (функция «штрих Шеффера»).
Функция «стрелка Пирса». Логическое выражение у =  читается как: у истинно, если обе входные величины ложны.
читается как: у истинно, если обе входные величины ложны.
Таблица состояний, ее релейный эквивалент и изображение бесконтактного логического элемента показаны на рис. 76, а, б, в.
Для реализации функции НЕ нужно подать один из сигналов, например xlt на один из входов (или на оба входа) элемента (рис. 76, г), тогда логическое уравнение элемента будет
 у=х1 + х1= x1
у=х1 + х1= x1
|
|
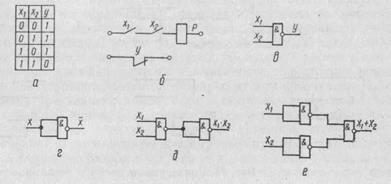
Функция И может быть реализована, если на вход элемента ИЛИ — НЕ подать предварительно инвертированные сигналы (рис. 76, д)
Рис. 77. Логический элемент И—НЕ:
а — таблица состояний; б — релейно-контактная схема; в — условное обозначение; г, д, е — реализация основных логических функций на элементах И—НЕ
Для реализации функции ИЛИ нужно подать входные сигналы на элемент ИЛИ — НЕ, а затем выходной сигнал первого элемента подать на оба входа второго элемента (рис. 76, е), тогда логическое выражение элемента будет
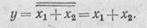
 Ф у н к ц и я «штрих Шеффера». Логическое выражение у=х1 + х2 читается как: у ложно, если обе входные величины истинны.
Ф у н к ц и я «штрих Шеффера». Логическое выражение у=х1 + х2 читается как: у ложно, если обе входные величины истинны.
Таблица состояний, ее релейный эквивалент и изображение бесконтактного элемента показаны на рис. 77, а, б, в.
Для реализации функции НЕ нужно подать сигнал, например x1 на оба входа элемента И — НЕ (рис. 77, г).
 у=х1 + х1= x1
у=х1 + х1= x1
Функция И может быть реализована, если подать входные сигналы на элемент И — НЕ, а затем выходной сигнал первого элемента подать на оба входа второго элемента (рис. 77, д):
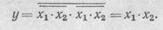
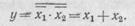
|
| Для реализации функции ИЛИ нужно подать на вход элемента И — НЕ предварительно инвертируемые сигналы (рис. 77, е): |
Циклограмма — это графическое изображение последовательности работы отдельных элементов логической системы управления во времени. Работа элементов дискретного действия в логическом устройстве характеризуется появлением и исчезновением сигналов в определенной последовательности.
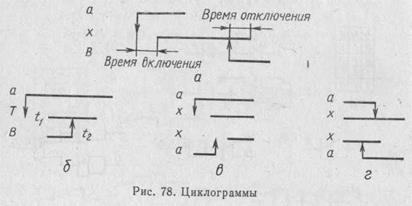
Наличие сигнала изображают на циклограмме отрезком горизонтальных линий. Слева от отрезка, отражающего работу элемента, на границе циклограммы проставляют обозначение соответствующего сигнала. Последовательность работы элементов определяется положением концов отрезков, изображающих их работу, относительно левой границы циклограммы. Циклограмма отражает любое изменение состояния элементов и указывает собственное время их срабатывания (рис. 78, а).
Воздействие одного элемента на другой изображают на циклограмме стрелкой, указывающей направление воздействия.
В циклограмме время не оценивается количественно, поэтому ее выполняют без масштаба. Различают лишь факт срабатывания элемента, факт наличия или отсутствия сигнала. При наличии специального элемента задержки его сигнал на циклограмме обозначают Т, а время, по истечении которого он появляется или исчезает, t (рис. 78, б).
На рис. 78, в показаны варианты воздействия элемента а на элемент х при его включении. В первом варианте элемент х включается при появлении сигнала а, во втором — при его исчезновении. На рис. 78, г показаны варианты воздействия элемента а на элемент х при его отключении.
Тактами называют периоды, в течение которых в схеме не изменяется состояние ни одного из входных, промежуточных или выходных сигналов. Каждое изменение состояния одного или
одновременно нескольких элементов является началом нового такта.
Периодом включения элемента называют непрерывный ряд тактов, в течение которого этот элемент находится во включенном состоянии. Период отключения элемента — непрерывный ряд тактов, в течение которого элемент находится в отключенном состоянии.
Включающим называют такт, предшествующий периоду включения данного элемента. Отключающим — такт, предшествующий периоду отключения данного элемента.
Включающий период состоит из включающего такта и периода отключения без включающего такта (понятие отключающего периода вводится при наличии нескольких периодов включения).
Методика заполнения циклограммы: 1) вычерчивают циклограмму с разбивкой на такты, но без нумерации; 2) слева записывают входные и выходные сигналы; 3) просматривают такты по вертикали, и в каждой строке в зависимости от состояния командного или исполнительного органа наносят или пропускают линию; 4) такту присваивают номер, если в такте появилась или исчезла хотя бы одна линия; 5) к изменившимся в такте выходным сигналам направляют стрелки от входных сигналов, вызвавших эти изменения; 6) заполненную циклограмму проверяют на повторяемость тактов — одинаковые такты не должны иметь разные номера; 7) отыскивают и объединяют в группу такты, многократно повторяющиеся.
Дата добавления: 2015-07-14; просмотров: 2065;
