ЭЛЕМЕНТЫ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ

Автоматическая система, которая обеспечивает лучшие показа­тели качества при заданных реальных условиях работы и ограни­чениях, называется оптимальной.

Достижение оптимального функционирования АСР во многом определяется тем, как осуществляется управление во времени, какова программа и алгоритм управления. Поэтому для оценки оптимальности систем используют интегральные критерии. В за­висимости от принятого критерия оптимальности рассматриваются следующие виды оптимальных систем:

1. Системы, оптимальные по быстродействию,— обеспечивают
минимальное время перехода объекта из одного состояния в дру­
гое. В этом случае критерий оптимальности I=t_K—t_H, где t_H и t_K—
время начала и конца процесса управления.

Следовательно, в таких системах обеспечивается минимальная длительность процесса управления. Простейший пример — си­стема управления электродвигателем, обеспечивающая минималь­ное время разгона до заданной частоты вращения с учетом всех имеющихся ограничений.

2. Системы, оптимальные по расходу ресурсов,— обеспечивают
минимум критерия

5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ НАСТРОЙКИ РЕГУЛЯТОРОВ ДЛЯ ОБЪЕКТОВ ПЕРВОГО ПОРЯДКА С ЗАПАЗДЫВАНИЕМ

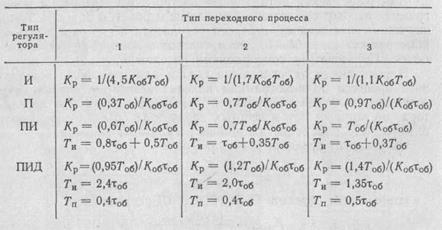
На третьем этапе определяют оптимальные значения параметров настройки регулятора и устанавливают их на реальной аппара­туре. Выбранные параметры настройки регулятора должны обес­печивать требуемое качество работы объекта управления.

На последнем этапе параметры настройки регулятора уточ­няются и корректируются в процессе эксплуатации системы управ­ления при различных режимах работы технологического объекта.

где К — коэффициент пропорциональности; U (t) — управляю­щее воздействие. Такие системы управления обеспечивают мини­мальный расход сырья, энергии и т. д. за все время управления технологическим объектом.

3. Системы оптимальные по точности —обеспечивают минималь­ные ошибки управления на основании критерия

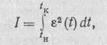
где 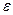(t) — динамическая ошибка.

Задача синтеза оптимальной системы автоматического управ­ления обычно формулируется следующим образом. Заданы мате­матическое описание объекта управления, граничные условия, включающие в себя цель управления и ограничения, которые на­ложены на выходную величину объекта, управляющие воздейст­вия, внешние возмущения и критерий оптимальности. Требуется найти управляющее устройство, обеспечивающее такое управле­ния объектом, при котором цель управления достигается при ми­нимальном значении критерия оптимальности и выполнении всех имеющихся ограничений.

Задача проектирования оптимальной АСР может быть решена простейшим методом перебора всех возможных вариантов. Хотя

такой метод требует больших затрат времени, но современные ЭВМ позволяют им воспользоваться. Для решения задач оптимизации разработаны специальные методы вариационного исчисления (ме­тод максимума, динамическое программирование и др.), позволяю­щие учесть все ограничения всех реальных систем.

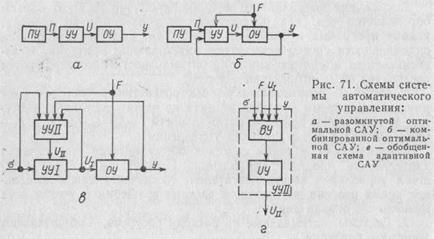
Как и обычные, оптимальные системы бывают разомкнутые, замкнутые и комбинированные. Если оптимальное управление, переводящее объект из начального состояния в конечное и неза­висящее или слабо зависящее от возмущающих воздействий, мо­жет быть задано как функция времени U = U (t), то строится ра­зомкнутая система программного управления (рис. 71, а). В про­граммное устройство ПУ закладывают оптимальную программу П, рассчитанную на достижение экстремума принятого критерия оп­тимальности.

По такой схеме осуществляется управление станками с число­вым программным управлением и простейшими работами.

Наиболее совершенными, хотя и более сложными, являются комбинированные оптимальные системы (рис. 71, б). В таких си­стемах разомкнутый контур осуществляет оптимальное управле­ние по заданной программе, а замкнутый контур, оптимизирован­ный по минимуму ошибки, отрабатывает отклонения выходных параметров. Используя канал измерения возмущений F, система становится инвариантной относительно множества задающих и воз­мущающих воздействий.

Для того чтобы реализовать столь совершенную систему уп­равления, необходимо точно и быстро измерять все возмущающие воздействия. Но это далеко не всегда возможно. Гораздо чаще известны только усредненные статистические характеристики воз­мущений. Во многих случаях даже задающее воздействие посту­пает в систему с помехами. А так как помеха представляет собой в общем случае случайный процесс, то удается синтезировать только

статистически оптимальную систему. Такая система не будет опти­мальной для каждой конкретной реализации процесса управления, но в среднем будет лучшей для всего множества его реализации.

Нередко встречаются объекты управления, у которых статиче­ские и динамические характеристики могут меняться в довольно широких пределах совершенно непредвиденно. Часто характери­стики объекта известны приблизительно, так же, как и возмущаю­щие воздействия, которые будут действовать в процессе эксплуа­тации. Обычные АСР здесь непригодны, необходимо, чтобы си­стема в процессе работы сама автоматически получала и использо­вала для выработки управляющих воздействий недостающую информацию. При этом система должна иметь способность к адап­тации путем изменения своих параметров или структуры при из­менении характеристик процесса или условий эксплуатации.

Таким образом, адаптивными называют системы, которые ре­шают задачи управления в неопределенных или переменных воз­действиях или параметрах объекта управления путем автоматиче­ской настройки. Фактическая возможность адаптации есть воз­можность автоматического управления автоматической системой. Поэтому в схеме адаптивной системы автоматического управления (рис. 71, в, г) появляется дополнительное устройство управления второго уровня УУII. Устройство управления первого уровня УУI в совокупности с объектом управления ОУ образует обычную АСР, но допускает возможность перестройки. Задачу УУII можно ус­ловно разбить на две части. В начале оно собирает информацию о работе основного контура управления, анализирует задающие и возмущающие воздействия (задача идентификации), а затем выраба­тывает управляющее воздействие U_II (задача автоматической на­стройки). Управление первым контуром производится на основа­нии критерия качества I его работы, подобного критерия оптималь­ности. Как и в неадаптивных системах, задачей управления может быть стабилизация или оптимизация этого критерия. Соответст­венно можно выделить адаптивные системы со стабилизацией и оптимизацией качества управления.