Глава 5
ВВЕДЕНИЕ В ТЕОРИЮ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
S 31. СПОСОБЫ ОПИСАНИЯ РАБОТЫ АВТОМАТИЧЕСКИХ
СИСТЕМ
В реальных условиях на ход протекающих технологических процессов влияют возмущающие воздействия — изменение количественных и качественных характеристик материальных потоков. Это приводит к нарушению нормального режима работы оборудования, т. е. к отклонению технологических переменных, характеризующих режим, от заданного значения. Для поддержания параметров на заданном уровне используют автоматические регуля-
торы, которые решают задачу стабилизации оптимальных режимов путем изменения количества регулируемой среды.
Описать работу автоматической системы можно словесно. Такое описание совершенно необходимо при решении любых задач, возникающих в автоматических системах, поскольку оно поясняет в первую очередь принцип действия конкретной системы.

|
Рассмотрим систему автоматического регулирования уровня жидкости H в баке (рис. 53). Возмущающими воздействиями являются изменения расхода. Если приток Qп равен расходу Qр, регулируемая величина Н в баке 1 объекта регулирования равна заданному значению Н3ад. При нарушении равенства Qп = Qр уровень изменяется, что приводит к рассогласованию  между текущим Н и Н3ад, т. е.
между текущим Н и Н3ад, т. е.  = =Н — Н3ад. При отклонении уровня поплавок 2 перемещает движок потенциометра 3, который совместно с потенциометром 4 образует мостовую схему. Напряжение разбаланса моста
= =Н — Н3ад. При отклонении уровня поплавок 2 перемещает движок потенциометра 3, который совместно с потенциометром 4 образует мостовую схему. Напряжение разбаланса моста 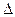 U подается на усилитель 5, на выходе которого включен реверсивный двигатель 6. Вал электродвигателя связан с вентилем 7, являющимся регулирующим органом автоматической системы регулирования (АСР) уровня.
U подается на усилитель 5, на выходе которого включен реверсивный двигатель 6. Вал электродвигателя связан с вентилем 7, являющимся регулирующим органом автоматической системы регулирования (АСР) уровня.
Направление вращения двигателя, а следовательно, открытие или закрытие вентиля 7 зависит от направления изменения уровня, т. е. от знака рассогласования  . При увеличении уровня
. При увеличении уровня  >0 вентиль уменьшит подачу Qп, при уменьшении уровня
>0 вентиль уменьшит подачу Qп, при уменьшении уровня  <0 подача увеличится. Заданное значение уровня Н3ад можно менять, перемещая движок потенциометра 4, что приводит к разбалансу моста, изменению притока Qп, а значит, и уровня Н.
<0 подача увеличится. Заданное значение уровня Н3ад можно менять, перемещая движок потенциометра 4, что приводит к разбалансу моста, изменению притока Qп, а значит, и уровня Н.
Словесное описание не может в полной мере характеризовать систему из-за отсутствия количественной оценки качества работы последней. Кроме того, существует много систем, различных как по назначению, так и по принципу действия, и описание каждой из них в отдельности не позволяет дать каких-либо обобщений и сравнить различные системы между собой. Поэтому для описания работы автоматических систем используются другие способы, позволяющие количественно и качественно описывать поведение системы как в установившемся, так и переходных режимах. Работу любой автоматической системы в установившемся и переходном режимах можно описать, использовав статические и динамические характеристики элементов системы.
Статической характеристикой называют зависимость выходного параметра от входного в установившемся режиме. Статические характеристики позволяют рассчитать величину изменения выходного параметра при известном изменении входного воздействия после достижения установившегося состояния.
Математическое выражение этой зависимости у = f (х) называют уравнением статики. На рис. 54 приведены примеры статических характеристик элементов автоматических систем, которые могут быть линейными и нелинейными.
Линейная статическая характеристика представляет собой прямую, проходящую под некоторым углом к оси абсцисс (рис. 54, а). Угол наклона характеристики есть величина постоянная, а его тангенс определяет величину коэффициента передачи или коэффициента усиления k элемента: k = y/x.
Для нелинейных статических характеристик коэффициент передачи в разных точках характеристики различен и определяется величиной тангенса угла наклона касательной к выбранной точке нелинейной характеристики.
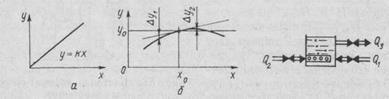
Рис. 54. Статические характеристики: линейная (а), нелинейная (б) Рис. 55. Технологический объект управления
Большинство реальных объектов управления обладают нелинейными статическими характеристиками, и их динамика описывается нелинейными дифференциальными уравнениями, решение которых весьма сложно. Поэтому важно рассмотреть возможность их линеаризации — замены нелинейной статической характеристики отрезками прямых линий. Линеаризация нелинейной статической характеристики возможна только в том случае, если она непрерывна и имеет непрерывное изменение производной во всем диапазоне кривой.
Для линеаризации заданной аналитически нелинейной статической характеристики у = f (х) ее раскладывают в окрестности значения входной величины х0 в ряд Тейлора:

и приближенно заменяют f (х) двумя первыми членами этого ряда
y 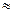 f(х0)+ f’(х0)(x -х0)
f(х0)+ f’(х0)(x -х0)
т. е. кривую f (х) заменяют прямой, касательной к ней в точке х0, с наклоном, соответствующим f’ (х0).
При линеаризации нелинейных характеристик предполагается, что отклонения переменных от их установившихся значений остаются достаточно малыми.
Если статическая характеристика задана графически, для ее линеаризации в рабочей точке с абсциссой х0 проводят касательную так, чтобы отрезки между кривой и касательной в диапазоне реальных изменений входной величины х1 и х2 были равны между собой 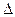 у1 =
у1 = 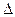 у2, как показано на рис. 54, б.
у2, как показано на рис. 54, б.
Допустимость замены нелинейной функции прямой линией оценивается по величине возможных ошибок из-за расхождения, приближенно их можно оценивать по величине 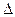 у1 =
у1 = 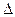 у2 на границе интервала изменения входной величины.
у2 на границе интервала изменения входной величины.
Динамические характеристики автоматической системы и ее элементов есть зависимости изменения выходного параметра во времени при известном законе изменения входного воздействия. Динамические свойства автоматической системы и ее элементов могут быть описаны дифференциальными уравнениями, передаточными функциями, временными и частотными характеристиками.
Дифференциальные уравнения автоматической системы и ее элементов.Для аналитического описания динамических свойств элементов автоматических систем дифференциальными уравнениями используют самые разнообразные физические, химические и другие законы. Наиболее часто применяют уравнения материального или энергетического балансов.
Рассмотрим пример составления дифференциального уравнения для некоторых простейших элементов систем автоматического регулирования. На рис. 55 в качестве элемента АСР показан объект регулирования, представляющий собой теплообменник, в который непрерывно подаются холодная вода и пар. Смешиваясь с горячим конденсатом, вода нагревается и, достигнув требуемой температуры, подается потребителю. Выходной величиной в этом объекте является температура горячей воды, а входной — поток тепла, поступающий в теплообменник с паром и холодной водой.
Обозначим через Q1 и Q2 количество тепла, поступающего в теплообменник в единицу времени с холодной водой и паром соответственно, Q3 —__количество тепла, выходящего из теплообменника в единицу времени с горячей водой.
При установившемся режиме потоки тепла, приходящие и уходящие в теплообменнике, равны между собой:  и температура горячей воды неизменна:
и температура горячей воды неизменна: 
Если изменить параметры какого-либо из тепловых потоков или всех одновременно, температура 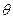 станет изменяться, скорость этого изменения будет зависеть от величины изменения тепловых потоков и коэффициента А тепловой емкости объекта, «спустя некоторое время установится температура, соответствующая новому балансу тепловых потоков. В переходном режиме от одного установившегося состояния в другое справедливо уравнение
станет изменяться, скорость этого изменения будет зависеть от величины изменения тепловых потоков и коэффициента А тепловой емкости объекта, «спустя некоторое время установится температура, соответствующая новому балансу тепловых потоков. В переходном режиме от одного установившегося состояния в другое справедливо уравнение
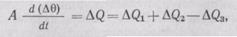
где 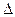 Q = Q—Qo — изменение теплового потока.
Q = Q—Qo — изменение теплового потока.
Предположим, что количество тепла, поступающего с холодной водой, неизменно, т. е. 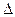 Q1 = 0, и возмущение наносится расходом пара Q2. Если принять во внимание, что изменение теплового потока
Q1 = 0, и возмущение наносится расходом пара Q2. Если принять во внимание, что изменение теплового потока 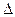 Q3 пропорционально изменению температуры горячей воды, ее удельной теплоемкости с и массе т, то
Q3 пропорционально изменению температуры горячей воды, ее удельной теплоемкости с и массе т, то 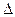 Q3 = cm
Q3 = cm 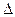
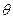 , и дифференциальное уравнение в переходном режиме будет:
, и дифференциальное уравнение в переходном режиме будет:
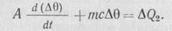
Обычно дифференциальные уравнения приводят к виду, при котором коэффициент при переменной 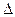
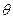 равен единице. Разделив обе части уравнения на тс, получим
равен единице. Разделив обе части уравнения на тс, получим
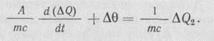
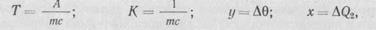
|
| тогда в общем виде дифференциальное уравнение рассмотренного элемента АСР можно записать в виде |
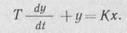
|
Введем обозначения:
Коэффициент Т — постоянная времени; К, — коэффициент передачи объекта регулирования.
Таким образом, динамические свойства смешивающего теплообменника описывают линейным дифференциальным уравнением первого порядка.
Дифференциальное уравнение элемента или всей автоматической системы может иметь более высокий порядок и содержать производные не только выходной (в левой части уравнения), но и входной величины (в правой части).
В общем случае автоматическая система может быть описана линейным дифференциальным уравнением с постоянными коэффициентами в виде
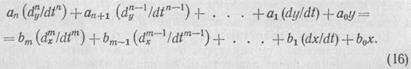
Решение дифференциальных уравнений высокого порядка вызывает значительные трудности из-за необходимости определения корней характеристического уравнения и постоянных интегрирования, поэтому часто интеграл дифференциального уравнения находят с помощью операторного метода Лапласа.
Передаточные функции.Это — особая форма записи преобразованного по Лапласу дифференциального уравнения. Использование передаточных функций дает ряд преимуществ при исследова-
нии процесса регулирования, т. е. при решении дифференциального уравнения динамики. Преобразование Лапласа позволяет представить функцию вещественного переменного (времени) как функцию комплексного переменного. Это осуществляют с помощью прямого преобразования Лапласа по формуле
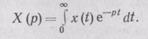
Исходная функция времени х (t) называется оригиналом, комплексная функция X (р) — изображением.
Сокращенно преобразование Лапласа записывают также в виде 
Если известно изображение X (р) и требуется получить функцию времени, то оригинал находят по правилам обратного преобразования Лапласа.
Рассмотрим основные свойства преобразования Лапласа.
1. Умножение оригинала на постоянную величину а соответст
вует умножению изображения на это же число: L [ax (t) ]= аХ (p)•
2. Суммирование оригиналов соответствует суммированию изо
бражений L [х1 (t) + х2 (t)] = Х1 (p) + Х2 (р).
3. Дифференцированию оригиналов соответствуют следующие
выражения для изображений:

При нулевых начальных условиях, если при t = 0 выходная величина х (0) и все ее производные х' (0) ... хn-1 (0) равны 0,
получим
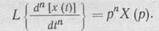
Таким образом, в этом случае n-кратному дифференцированию оригинала соответствует просто умножение на рп его изображения.
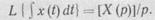
|
| Пользуясь свойствами преобразования Лапласа 1, 2 и 3 при нулевых начальных условиях дифференциальное уравнение си- |
4. Интегрирование интеграла соответствует делению изображения на р
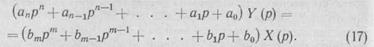
|
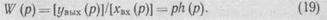
|
| стемы (16) можно привести к виду |
Таким образом, в области изображений дифференциальные уравнения превращаются в алгебраические, а операции дифференцирования и интегрирования заменяются соответственно умножением или делением на оператор р. Это не только упрощает процесс решения сложных задач, но и открывает новые возможности переработки информации о динамических свойствах сложных систем по заданным характеристикам элементов системы.
Решение дифференциального уравнения с помощью преобразований Лапласа основано на том, что в заданном уравнении выражения для неизвестной функции и ее производных, а также функций, характеризующих возмущающее воздействие, заменяют соответствующими изображениями. Таким образом получается вспомогательное уравнение в изображениях — алгебраическое. Из этого уравнения находят изображение искомой функции.
Основная трудность при использовании этого метода заключается не в решении уравнения, а в переходах от оригинала функции к ее изображению и обратно. Практические операции прямого и обратного преобразования Лапласа осуществляют с помощью таблиц оригиналов и изображений, приводимых в справочниках.
Полученное вспомогательное уравнение (17) в изображениях несет ту же информацию о динамике системы, что и исходное дифференциальное. Но поскольку это уравнение алгебраическое, появляется возможность динамику системы характеризовать отношением изображений выходного сигнала Y (р) к входному X (р). Такое отношение представляет собой алгебраическое выражение и с его помощью простейшим образом непосредственно (не переходя к оригиналу решения) могут быть получены выражения, характеризующие как динамические, так и статические свойства анализируемой системы. Это отношение называют передаточной функцией системы
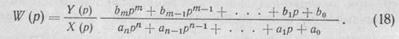
Из выражения (18) и определения передаточной функции следует, что Y(p) = W(p) X (р), т. е. изображение выходной величины равно произведению изображения входной величины на передаточную функцию этого элемента или системы.
Передаточные функции широко используются при исследовании автоматических систем регулирования. На изучении ее свойств основаны все современные методы анализа качества автоматических систем, не требующие непосредственного решения дифференциального уравнения.
Временные характеристики автоматической системы и ее элементов.Временными характеристиками системы называют зависи-
мости от времени значений выходной величины при поступлении на вход некоторого типового воздействия. Наиболее важная временная характеристика — реакция системы на единичное ступенчатое воздействие входной величины, так как этот режим работы наиболее часто возникает в системе при ее включении, изменении режима и т. д. Таким образом, под временной характеристикой понимается процесс изменения выходной величины в функции времени при переходе системы из одного равновесного состояния в другое в результате поступления на вход единичного ступенчатого воздействия.
Дифференциальное уравнение системы тоже определяет изменение выходной величины во времени, поэтому временная характеристика представляет собой графическое решение дифференциального уравнения системы для единичного входного воздействия при нулевых начальных условиях, и следовательно, характеризует динамические свойства системы.
Так как временные характеристики системы могут быть получены не только путем решения дифференциального уравнения системы, но и экспериментально, то возможность изучения динамики системы по временной характеристике имеет важное практическое значение, поскольку в этом случае не требуется находить и решать дифференциальные уравнения.
Если в течение всего времени перехода системы из одного устойчивого состояния в другое единичное входное воздействие (рис. 56, а)
XBX= 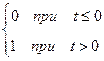
остается приложенным к звену или системе, то в этом случае временную характеристику принято называть переходной функцией элемента или системы. Графическое изображение переходной функции называют переходной характеристикой системы. Реакция системы на единичное ступенчатое воздействие в виде дельта-функции (рис. 56, б)
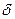 (t)=
(t)= 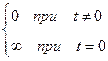
называется импульсной переходной функцией. Ее графическое изображение называется импульсной переходной характеристикой элемента или системы.

|
| С учетом этих соотношений получаем |
При поступлении на вход элемента или разомкнутой системы с передаточной функцией W (р) входной величины хвх0 = 1 на выходе получаем временную характеристику увых (t) = h(t). При этом изображения входной и выходной величины равны:
Из выражения (19) следует, что по временной характеристике системы можно получить передаточную функцию системы.
Частотные характеристики автоматических систем и их элементов. Для описания поведения системы и ее элементов широко используют частотные характеристики, которые определяют их динамику при воздействии на их вход гармонических колебаний вида xВХ (t) = AВХl sin ( 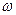 1t), где AВХl— амплитуда входных колебаний;
1t), где AВХl— амплитуда входных колебаний;  1 — угловая частота колебаний; t— время.
1 — угловая частота колебаний; t— время.
Если автоматическая система линейная, то на ее выходе также устанавливаются синусоидальные колебания с частотой  1; но с амплитудой AВХl. сдвинутые по фазе относительно входного сигнала на угол
1; но с амплитудой AВХl. сдвинутые по фазе относительно входного сигнала на угол  (рис. 57): уъых (t) = = AВХl sin (
(рис. 57): уъых (t) = = AВХl sin (  1t—
1t—  1).
1).
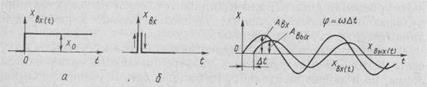
Рис. 56. Типовые входные воздействия: скачкообразное (а), импульсное (б) Рис. 57. Входные и выходные величины
Амплитуда Авых1 и фаза  1 выходных колебаний зависят от динамических свойств системы, частоты и амплитуды входных колебаний. Знак минус перед
1 выходных колебаний зависят от динамических свойств системы, частоты и амплитуды входных колебаний. Знак минус перед 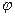 обусловлен тем, что у реальных элементов автоматических систем выходное колебание отстает по фазе от входного.
обусловлен тем, что у реальных элементов автоматических систем выходное колебание отстает по фазе от входного.
Запишем хвх (t) и увых (t) в комплексном виде:
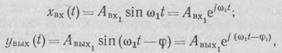
где j = 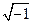 ,
,
Отношение выходных колебаний системы увых (t) к входным хвх (t), выраженным в комплексном виде, называют комплексным коэффициентом передачи системы при частоте 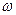 1
1

С изменением частоты колебаний на входе при постоянной амплитуде Aвх амплитуда выходных колебаний Aвых и фазовый сдвиг 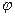 будут меняться, что вызовет изменение комплексного коэффициента передачи системы. Совокупность всех значений комплексного коэффициента передачи при изменении
будут меняться, что вызовет изменение комплексного коэффициента передачи системы. Совокупность всех значений комплексного коэффициента передачи при изменении  от 0 до
от 0 до  называют комплексной частотной характеристикой системы или амплитудно-фазовой характеристикой (АФХ) системы и обозначают через W (j
называют комплексной частотной характеристикой системы или амплитудно-фазовой характеристикой (АФХ) системы и обозначают через W (j  ),
),
Зависимость отношения амплитуд выходных и входных колебаний от частоты  называют амплитудно-частотной характеристикой (АЧХ) и обозначают через А (
называют амплитудно-частотной характеристикой (АЧХ) и обозначают через А ( 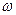 ) (рис. 58, о). Зависимость фазового сдвига выходных колебаний относительно входных
) (рис. 58, о). Зависимость фазового сдвига выходных колебаний относительно входных 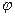 от частоты колебаний
от частоты колебаний 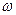 называют ф а з о -частотной характеристикой (ФЧХ) и обозначают через
называют ф а з о -частотной характеристикой (ФЧХ) и обозначают через 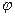 (
(  ) (рис. 58, б). Эти частотные характеристики связаны между собой уравнением
) (рис. 58, б). Эти частотные характеристики связаны между собой уравнением

Графически АФХ представляет собой кривую, называемую годографом, описываемую на комплексной плоскости концом вектора, модуль которого равен значениям A(  ), а аргумент —
), а аргумент —  (
(  ) при изменении частоты
) при изменении частоты 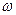 от 0 до
от 0 до 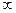 (рис. 58, в).
(рис. 58, в).
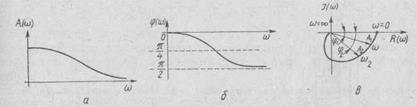
Рис. 58. Частотные характеристики: амплитудно-частотная (а), фазо-частот-ная (б), амплитудно-фазовая (в)
Проекцию АФХ на действительную ось комплексной плоскости называют вещественной частотной характеристикой и обозначают через R ( 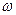 ), а проекцию на мнимую ось — мнимой частотной характеристикой и обозначают через I (
), а проекцию на мнимую ось — мнимой частотной характеристикой и обозначают через I ( 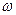 ).
).
Частотные характеристики могут быть определены одна через другую с помощью следующих зависимостей:
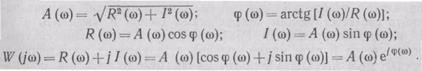
Частотные характеристики могут быть получены экспериментально или из дифференциального уравнения системы. Если задана
то для получения 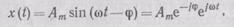 производной ее надо умножить на функцию j
производной ее надо умножить на функцию j 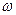
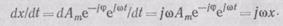
Для получения второй производной функцию умножают на (j 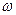 )2: (d2x)/(dt2) = (j
)2: (d2x)/(dt2) = (j 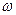 )2х и т. д.
)2х и т. д.
Подставив в дифференциальное уравнение выражения для входных и выходных установившихся колебаний, получим АФХ:
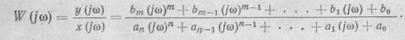
Таким образом, для получения АФХ достаточно в передаточную функцию системы вместо оператора р подставить j  . При этом необходимо избавиться от мнимости в знаменателе, для чего дробь умножают и делят на комплексно-сопряженный знаменателю член.
. При этом необходимо избавиться от мнимости в знаменателе, для чего дробь умножают и делят на комплексно-сопряженный знаменателю член.
§ 32. СТРУКТУРНЫЕ СХЕМЫ И ИХ ПРЕОБРАЗОВАНИЕ
Структурная схема системы автоматического управления представляет собой ее динамическую модель и состоит из отдельных типовых динамических звеньев, отражающих динамические свойства системы в целом.

Рис. 59. Способы соединений звеньев: последовательное (а), параллельное (б), последовательно-параллельное (в)
Чтобы получить структурную схему автоматической системы управления, необходимо каждый ее функциональный элемент заменить соответствующим динамическим звеном и соединить их в той же последовательности. Графически структурная схема системы изображается в виде прямоугольников, в которых записываются передаточные функции звеньев. Связи между звеньями обозначаются линиями со стрелками, указывающими направление передачи сигнала.
Звенья, образующие структурную схему, могут быть соединены между собой последовательно, параллельно или встречно-параллельно. Зная передаточные функции отдельных звеньев, образующих структурную схему системы, и пользуясь определенными правилами эквивалентного преобразования структурных схем, можно получить передаточную функцию системы любой сложности и упростить структурные схемы системы в целом.
Последовательное соединение звеньев.Последовательным называется такое соединение звеньев системы, при котором выход каждого предыдущего связан с входом последующего звена (рис. 59, а). При таком соединении звеньев все воздействия передаются после-
довательно от одного звена к другому. При последовательном соединении п звеньев с передаточными функциями W1 (p), W2 (р) . . . . . . Wn (p) будем иметь следующую систему уравнений:
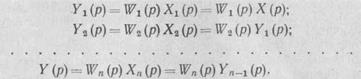
Решая эту систему уравнений относительно входной X (р) и выходной Y (р) величин, получим
Y(p) = W1(p)W2(p). . .Wn(p)X(p). Передаточная функция системы в целом
W(p)=[Y(p)]/[X(p)]=W1(p) W2,(p). . .Wn(p),
следовательно, передаточная функция автоматической системы, состоящей из п последовательно соединенных звеньев, равна произведению передаточных функции всех звеньев, входящих в соединение.
Параллельное соединение звеньев.Параллельным называется такое соединение, при котором входные воздействия всех звеньев одинаковы, а выходная величина системы равна сумме выходных величин отдельных звеньев (рис. 59, б). Так, для системы, состоящей из n параллельно соединенных звеньев, можно записать:

Решая эту систему уравнений относительно Y (р) и X (р), получим
Y(p) = [W1(p) + W2(p)+ . . . +Wn(p)]Y(p).
Следовательно, систему, состоящую из п параллельно соединенных звеньев, можно заменить одним эквивалентным звеном, передаточная функция которого
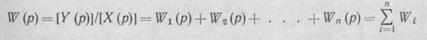
равна сумме передаточных функций всех звеньев, входящих в это соединение.
Встречно-параллельное соединение звеньев.Если выходная величина одного звена подается на вход другого, а входная величина первого звена формируется в виде суммы его входного воздействия и выходного воздействия второго звена, как это показано
на рис. 59, в, то такое соединение называют встречно-параллельным или обратной связью.
Обратной связью называется цепь передачи воздействий с выхода системы (звена) на ее вход. Обратная связь будет положительной, если выходная величина ее звена суммируется с входной величиной системы, и отрицательной, если выходная величина цепи обратной связи вычитается из входной величины. На вход первого звена, стоящего в прямой цепи системы, подается сигнал  Х (р), равный
Х (р), равный  Х (р) = X (р) ± Хо.с (р).
Х (р) = X (р) ± Хо.с (р).
Для системы, показанной на рис. 59, в, с отрицательной обратной связью будем иметь следующую систему уравнений:
Решая эту систему уравнений, получим
Y (Р) = [W1 (p) /(1 + W1 (p) W2 (p)] X (р).
Следовательно, систему с обратной связью можно заменить одним эквивалентным звеном, передаточная функция которого

Используя полученные выражения для преобразования структурных схем, можно определить передаточные функции любой автоматической системы.
§ 33. КЛАССИФИКАЦИЯ ЗВЕНЬЕВ ПО ДИНАМИЧЕСКИМ СВОЙСТВАМ
При решении задач анализа и синтеза автоматическую систему
разбивают на отдельные части, математическая зависимость между
входными и выходными величинами которых и временем описы
вается дифференциальными уравнениями не выше второго порядка.
Такие искусственно выделенные части автоматической системы на
зывают элементарными динамическими
звеньями. В отличие от элемента динамическое звено необя
зательно является конструктивной или схемнозаконченной частью
системы. Одному элементу (например, исполнительному механизму)
могут соответствовать несколько динамических звеньев.
При представлении элементов системы в виде элементарных динамических звеньев не важен принцип построения элемента. Элементы различной физической природы могут быть представлены в виде одинаковых динамических звеньев, если их динамические свойства описываются одинаковыми дифференциальными уравнениями. Поэтому при решении задач анализа и синтеза автоматических систем многообразие элементов автоматики сводится к нескольким типовым элементарным динамическим звеньям.
Существуют 6 типовых элементарных динамических звеньев: усилительное, апериодическое, колебательное, интегрирующее, дифференцирующее и чистого запаздывания.
Усилительное звено.Это простейшее звено, которое образуется в случае передачи входного сигнала на выход без каких-либо замедлений или ускорений во времени, т. е. переходные процессы в звене отсутствуют. Примеры усилительных звеньев приведены на рис. 60, а—в.
Свойства этого элемента описываются уравнением у = Кх, где К — коэффициент усиления звена.
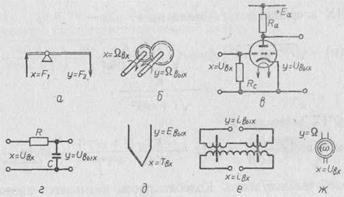
Рис. 60. Усилительные и апериодические звенья:
а — рычажная передача; б — зубчатая пара; в — усилитель; г — пассивный четырехполюсник; д — термопара; е — магнитный усилитель; ж — электродвигатель
Передаточная функция звена представляет собой постоянную величину W (р) = К.
Амплитудно-фазовая характеристика усилительного звена также равна постоянной величине W (j  ) = К, при этом амплитудно-частотная характеристика А (
) = К, при этом амплитудно-частотная характеристика А (  ) = К, а фазочастотная характеристика
) = К, а фазочастотная характеристика  (
(  ) = 0. Графически АФХ изображается в виде точки на вещественной оси комплексной плоскости на расстоянии К от начала координат.
) = 0. Графически АФХ изображается в виде точки на вещественной оси комплексной плоскости на расстоянии К от начала координат.
Апериодическое звено.Звено называется апериодическим, если его входная и выходная величины связаны между собой дифференциальным уравнением
T(dy)/dt + y = Kx.
Примеры апериодических звеньев приведены на рис. 60, г—ж. В операторной форме это уравнение может быть записано как
(Tp+1)Y(p) = KX(p),
тогда передаточная функция звена имеет вид
W(p) = K/(Tp+1).
Если на вход звена Подать ступенчатое воздействие, то временная характеристика будет иметь вид
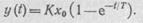
Заменив р на j  , получим АФХ апериодического звена
, получим АФХ апериодического звена
При Т1 = 2Т2 получают вещественные и равные корни уравнения  а временная характеристика записывается выражением
а временная характеристика записывается выражением
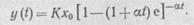
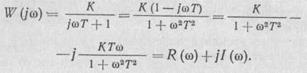
|
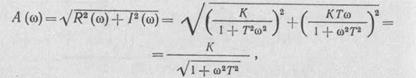
|
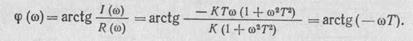
|
| АЧХ апериодического звена имеет вид |
| а ФЧХ этого звена |
Колебательное звено.Колебательным называется звено, у которого выходные и входные величины связаны следующим дифференциальным уравнением:
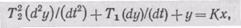
которое в операторном виде записывается как
Передаточная 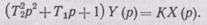 функция колебательного звена имеет вид
функция колебательного звена имеет вид
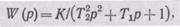
где К — коэффициент усиления звена; Т1иТ2 — постоянные времени звена; при Т2 = 0 звена превращается в апериодическое.
Примеры некоторых колебательных звеньев приведены на рис. 61.
В зависимости от соотношения между постоянными времени Т1 и Т2 корни характеристического уравнения  будут вещественными, мнимыми или комплексно-сопряженными. В соответствии с этим и временная характеристика звена будет иметь апериодический или колебательный характер.
будут вещественными, мнимыми или комплексно-сопряженными. В соответствии с этим и временная характеристика звена будет иметь апериодический или колебательный характер.
При Т1>2Т2 получают вещественные и разные корни р1 = 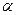 1 и р2 =
1 и р2 = 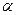 2 характеристического уравнения, тогда временная характеристика звена имеет вид
2 характеристического уравнения, тогда временная характеристика звена имеет вид
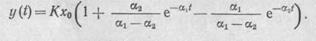
При Т1 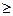 2Т2 переходные процессы в звене протекают апериодически и такое звено не является колебательным. Оно может быть представлено в виде последовательного соединения двух апериодических звеньев.
2Т2 переходные процессы в звене протекают апериодически и такое звено не является колебательным. Оно может быть представлено в виде последовательного соединения двух апериодических звеньев.
При T1<2Т2 корни уравнения будут комплексными p1,2 =
= 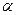 ±j
±j  , где
, где 
|
|
Временная характеристика такого звена
Рис. 61. Колебательные звенья:
а — пассивный четырехполюсник; б — мембранный исполнительный механизм
При Т1 = 0 в колебательном звене возникают незатухающие колебания. АФХ колебательного звена имеет вид
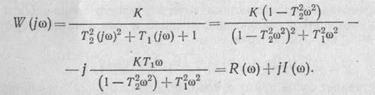
Амплитудно-частотная и фазочастотная характеристики колебательного звена:
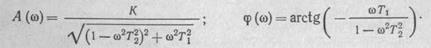
Интегрирующеезвено. Звено называется интегрирующим, если выходная величина пропорциональна интегралу от входной величины.
Дифференциальное уравнение интегрирующего звена имеет вид
T(dy)/(dt) = Kx.
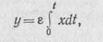
|
где  = K/T — скорость разгона. = K/T — скорость разгона.
|
Интегрируя это уравнение, получим
Рис. 62. Интегрирующие, дифференцирующие и запаздывающие звенья:
а— пассивный четырехполюсник; б — гидравлический исполнительный механизм; в—электродвигатель; г - пассивный четырехполюсник; д - спокоитель с пружиной в механических цепях; е — ленточный конвейер
Примеры некоторых интегрирующих звеньев приведены на рис. 62, а—в.
Передаточная функция такого звена: W (р) =  /р.
/р.
Временная характеристика интегрирующего звена у (t) = 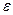 xot имеет вид прямой линии, наклоненной к оси абсцисс под углом а = arctg
xot имеет вид прямой линии, наклоненной к оси абсцисс под углом а = arctg 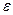 x0. АФХ звена
x0. АФХ звена
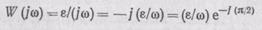
представляет собой прямую, совпадающую с отрицательной мнимой осью характеристики. Амплитуда выходных колебаний звена А (  ) =
) = 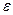 /
/  убывает с частотой, а фаза
убывает с частотой, а фаза 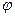 = —
= — 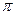 /2. Таким образом, интегрирующее звено при всех частотах создает отставание выходных колебаний от входных на 90°.
/2. Таким образом, интегрирующее звено при всех частотах создает отставание выходных колебаний от входных на 90°.
Дифференцирующее звено.Динамическая характеристика этого звена описывается дифференциальным уравнением вида у =
= К (dx)/(dt), и передаточная функция этого звена равна
W (р) = Кр.
Дифференцирующее звено представляет собой устройство, которое на выходе дает величину, производную по времени от входной величины. Однако на практике осуществить такое идеальное дифференцирующее звено невозможно, так как все физические процессы в природе в той или иной степени инерционны, а в соответствии с уравнением этого звена скачкообразное изменение входной величины должно вызвать мгновенное изменение выходной величины от 0 до 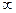 и немедленный спад ее до 0. В системах регулирования применяют звенья, которые выполняют дифференцирующее действие приближенно; они называются реальными дифференцирующими звеньями. Уравнение такого звена имеет вид
и немедленный спад ее до 0. В системах регулирования применяют звенья, которые выполняют дифференцирующее действие приближенно; они называются реальными дифференцирующими звеньями. Уравнение такого звена имеет вид
T(dy)/(dt) + y = KT(dx)/(dt),
а передаточная функция такого звена W (р) = (КТр)/(Тр + 1).
Временная характеристика реального дифференцирующего звена у (t) = Кхое—(t/T).
Примеры дифференцирующих звеньев приведены на рис. 62, г, д.
При уменьшении постоянной времени Т реальное дифференцирующее звено по своим свойствам приближается к идеальному.
АФХ реального дифференцирующего звена имеет вид

а АЧХ и ФЧХ определяются уравнениями:

Запаздывающее звено.Запаздывающим называют звено, вкотором выходная величина воспроизводит изменение входной величины без искажений, но с некоторым постоянным запаздыванием 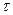 : y(t) = x (t—
: y(t) = x (t— 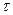 ).
).
Передаточная функция запаздывающего звена: W(p) = e—p/ 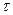 .
.
Примером запаздывающего звена может служить ленточный конвейер (рис. 62, е), который загружают с одного конца материалом, поступающим из бункера.
АФХ такого звена
W(j  )=e—j
)=e—j 
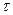
Графически ее представляют в виде окружности единичного радиуса А (  ) = 1 с центром в начале координат.
) = 1 с центром в начале координат.
§ 34. ХАРАКТЕРИСТИКИ АВТОМАТИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ
Совокупность устройств, подключаемых к объекту управления для автоматического регулирования его параметров, называется автоматическим регулятором. Непосредственно с объектом управления связаны измерительный элемент и исполнительный механизм регулятора. Входной величиной регулятора является регулируемый параметр, выходной — положение регулирующего органа.
Автоматические регуляторы и законы регулирования.Автоматический регулятор измеряет отклонение регулируемого параметра от заданного значения и в соответствии с реализованным законом регулирования воздействует на регулирующий орган для уменьшения этого отклонения. В промышленности для автоматизации различных технологических процессов используют множество регуляторов, отличающихся друг от друга разнообразными признаками.
Автоматические регуляторы классифицируют по следующим наиболее характерным признакам:
по назначению — регуляторы температуры, давления и т. д.;
в зависимости от источника энергии — регуляторы прямого и непрямого действия;
по конструктивному оформлению — регуляторы приборного типа, в котором все основные элементы смонтированы в одном корпусе, и агрегатные, состоящие из отдельных унифицированных блоков, каждый из которых имеет определенное назначение, что дает возможность разрабатывать схемы регулирования любой сложности;
по виду используемой энергии — регуляторы электрические, пневматические, гидравлические и комбинированные.
Основной характеристикой регулятора является реализованный в нем закон регулирования — зависимость между изменением регулируемого параметра и положением регулируемого органа. По характеру воздействия на регулируемый орган различают регуляторы непрерывного и дискретного действия.
Основными элементами регулятора являются (рис. 63):
измерительное устрoйство ИУ для измерения регулируемой величины; задающее устройство ЗУ для ручного или автоматического ввода заданного значения регулируемой величины;
устройство сравнения УС измеряемого и заданного значений для определения величины и знака отклонения; управляющее устройство УУ для вычисления величины регулирующего воздействия; исполнительный механизм ИМ для управления регулирующим органом РО на входе технологического объекта.
Регуляторы непрерывного действия в зависимости от реали
зуемого закона регулирования подразделяются на следующие
типы: интегральные — И-регуляторы; пропорциональные — П-ре-
гуляторы; пропорционально-интегральные — ПИ-регуляторы;
пропорционально-интегрально-дифференциальные — ПИД-регуля-торы.
Пропорциональными, или статическими, регуляторами называют такие регуляторы, у которых положение регулирующего органа пропорционально отклонению регулируемого параметра от заданного значения: х = — Кру, где Кр — коэффициент передачи регулятора, являющийся показателем его настройки.
Передаточная функция П-регулятора имеет следующий вид: W(p) = - Кр.
Преимуществом П-регулятора является его быстродействий, т. е. малое время переходного процесса и высокая устойчивость процесса регулирования. Основным недостатком П-регулятора является наличие остаточного отклонения регулируемого параметра, что снижает точность регулирования.
Интегральными, или астатическими, называются регуляторы, у которых при отклонении регулируемого параметра от заданного значения регулируемый орган перемещается до тех пор, пока регулируемый параметр не вернется к заданному значению. В таких регуляторах скорость перемещения ре-

Рис. 63. Структурная схема регулятора
Рис. 64. Характеристики переходного процесса для различного типа регуляторов:
1 — отсутствие регулятора; 2 — П-регулятор; 3 — И-регулятор; 4 — ПИ-регулятор;
5 — ПИД-регулятор
гулирующего органа пропорциональна величине отклонения регулируемого параметра от заданного значения: (dx)/(df) = — Тиу. Проинтегрировав это выражение, получим

где Tи — постоянная времени, представляющая собой время, за которое регулирующий орган переместится из одного крайнего положения в другое при максимальном отклонении регулируемого параметра от заданного значения. Параметр Tи является показате- лем настройки И-регулятора.
И-регулятор достаточно точно поддерживает заданное значение регулируемого параметра, но процесс регулирования протекает достаточно медленно, поэтому его используют в объектах с большим самовыравниванием, с незначительным запаздыванием и малыми по величине отклонениями.
Пропорционально-интегральные, или изо-д р о м н ы е, регуляторы характеризуются тем, что при отклонении регулируемой величины от заданного значения они вначале перемещают регулирующий орган пропорционально отклонению (как П-регулятор), а затем при подходе регулируемой величины к заданному значению медленно доводят ее до этого значения (как И-регулятор). Такое регулирование достаточно точно и быстродействующе.
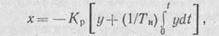
|
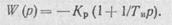
|
| Регулятор, действующий по такому принципу, называется ПИ-регулятором. Такие регуляторы действуют по следующему закону регулирования |
| где Kр — коэффициент передачи регулятора; Ти — время изодрома; KР и Ти — показатели настройки регулятора. Передаточная функция ПИ-регулятора имеет вид |
ПИ-регуляторы применяют в случаях, когда необходима большая точность регулирования и быстродействие.
Пропорционально-интегрально - дифференциальные регуляторы осуществляют закон регулирования, в котором регулирующий орган перемещается пропорционально отклонению, интегралу и скорости отклонения регулируемого параметра:
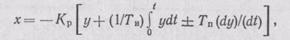
где KР — коэффициент передачи регулятора; Tи — время изодрома; ТП — время предварения.
Параметры КР, Ти, ТП являются показателями настройки ПИД-регулятора. Передаточная функция такого регулятора имеет вид

ПИД-регуляторы сложнее других регуляторов в настройке, однако они могут обеспечивать более высокое динамическое качество систем регулирования.
На рис. 64 для сравнения приведены характеристики П-, И, ПИ- и ПИД-регуляторов; на входе регуляторам приложено скачкообразное изменение возмущающего воздействия, объект управления для всех регуляторов один и тот же. Показано, как изменяется регулируемая величина для регуляторов различного типа, а также при отсутствии регулятора. При П-регуляторе в установившемся режиме остается некоторое отклонение регулируемой величины от заданного значения, при И-регуляторе это отклонение сводится к нулю. ПИ- и ПИД-регуляторы обеспечивают лучшее динамическое качество.
Регуляторы дискретного действия подразделяются на релейные и импульсные. В таких регуляторах регулирующий орган перемещается через определенные промежутки времени. Регулирующий орган изменяет свое положение («Открыто-Закрыто», «Мин.-Макс.» и др.) при достижении регулируемым параметром некоторых значений, именуемых пороговыми. Поэтому такие регуляторы называют позиционными. Они бывают двух- или
трехпозиционными. Релейные регуляторы применяются при малом запаздывании и большой постоянной времени объекта управления.
В импульсных регуляторах содержится импульсный элемент, преобразующий непрерывное изменение регулируемого параметра в ряд импульсов, следующих друг за другом через определенные промежутки времени. Импульсы могут отличаться амплитудой, длительностью и знаком в зависимости от конструкции регулятора.
Импульсные регуляторы обычно применяют для регулирования медленно протекающих процессов в инерционных объектах со значительным запаздыванием.
Задачей автоматической системы регулирования является поддержание заданных значений регулируемых величин технологического процесса или изменения их по определенному закону. В результате возникновения в системе возмущающих воздействий или изменения заданного значения регулируемой величины нарушается равновесие в системе, что вызывает переходный процесс, которыл приводит к новому равновесному состоянию. Характер переходного процесса определяется динамическими свойствами системы, в основе которых лежит понятие об ее устойчивости.
Устойчивость АСР.Устойчивостью называют способность системы восстанавливать состояние равновесия, из которого она была выведена в результате какого-либо воздействия.
Устойчивость является одним из основных показателей АСР, определяющих ее работоспособность. Поэтому при исследовании системы необходимо проводить анализ ее устойчивости. Автоматическая система будет устойчивой, если ее выходная величина остается ограниченной при любых ограниченных по абсолютной величине входных воздействий. Система будет неустойчивой, если при сколь угодно малых отклонениях от состояния равновесия она не возвращается к нему, а совершает около него недопустимо большие колебания или непрерывно удаляется от него. Такие системы не работоспособны.
Поведение автоматической системы регулирования при наличии в ней возмущающих и управляющих воздействий описывается дифференциальным уравнением
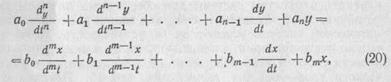
где а0, a1 . . . , ап и bо, b1 . . . , bm — постоянные коэффициенты. Процесс регулирования определяется решением этого дифференциального уравнения (20), представляющего собой сумму частного решения неоднородного уравнения (20) с правой частью и общего решения уравнения (20) без правой части, т. е.
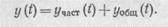
Первое слагаемое этого уравнения называется вынужденным решением (в случае yчаст (t) = const это будет установившееся значение), а второе слагаемое — переходной составляющей.
Система будет устойчивой, если стечением времени при t 
 переходная составляющая будет стремиться к нулю. Найдем эту составляющую из уравнения (20). Для этого необходимо решить характеристическое уравнение этой системы: аорn + а1рn-1 + . . . + + ап-1p + ап = 0. тогда общее решение уравнения (6—5) будет иметь вид:
переходная составляющая будет стремиться к нулю. Найдем эту составляющую из уравнения (20). Для этого необходимо решить характеристическое уравнение этой системы: аорn + а1рn-1 + . . . + + ап-1p + ап = 0. тогда общее решение уравнения (6—5) будет иметь вид:

где С1; С2 , . . . , Сп — постоянные коэффициенты; pl р2, . . . … , рп — корни характеристического уравнения системы.
Так как по условию задачи величина yобщ(t) с течением времени должна стремиться к нулю, то каждый член выражения (21) также должен стремиться к нулю. Для этого необходимо и достаточно, чтобы вещественная часть (действительные корни могут рассматриваться как частный случай комплексных корней с нулевой мнимой частью) всех корней характеристического уравнения была отрицательной. В этом случае показатели степени всех экспонент будут отрицательными, в результате чего с течением времени абсолютные значения всех экспоненциальных слагаемых будут стремиться к нулю.
Если хотя бы один корень характеристического уравнения имеет положительную или равную нулю вещественную часть, соответствующая составляющая переходного процесса CkePkt будет неограниченно возрастать или совершать незатухающие колебания. Следовательно, система не сможет прийти в установившееся состояние, т. е. система будет неустойчивой.
Таким образом, чтобы ответить на вопрос, устойчива или неустойчива система, достаточно найти корни ее характеристического уравнения. Однако этим методом пользоваться во многих случаях практически невозможно, так как находить корни алгебраических уравнений высоких степеней очень трудно. Кроме того, найдя корни характеристического уравнения, мы определим, устойчива или неустойчива система, но не сможем установить, как нужно изменить параметры системы для обеспечения или повышения ее устойчивости, и представить себе, как те или иные параметры автоматической системы влияют на ее устойчивость. Поэтому желательно иметь критерии, спомощью которых можно судить об устойчивости системы непосредственно по коэффициентам характеристического уравнения без вычисления корней. Поэтому в теории автоматического регулирования и инженерной практике широко применяют косвенные методы исследования системы автоматического регулирования на устойчивость. Такие критерии называются критериями устойчивости.
Критерии устойчивости АСР.Известны несколько таких критериев. Наиболее употребительны алгебраические критерии Рауса— Гурвица, основанные на рассмотрении системы неравенств, обра-
зуемых из коэффициентов характеристического уравнения, а также связанные с частотными представлениями критерии Михайлова и Найквиста.
Проверка устойчивости по критерию Рауса — Гурвица сводится к вычислению по коэффициентам характеристического уравнения так называемых определителей Гурвица, которые для устойчивой системы управления должны быть положительными. Иными словами, система устойчива, если определители  1;
1;  2, . . . ,
2, . . . , 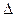 n, составленные из коэффициентов уравнения аорп + а1рп-х + а2рп-2 + ...+ ап-1р + ап = 0, положительны при ао>0.
n, составленные из коэффициентов уравнения аорп + а1рп-х + а2рп-2 + ...+ ап-1р + ап = 0, положительны при ао>0.
Для получения определителей Гурвица составляется таблица из коэффициентов характеристического уравнения п-й степени:

Правила составления таблицы: по главной диагонали выписывают по порядку п коэффициентов характеристического уравнения от а1 до ап; каждая строка содержит п элементов; строки с нечетными и четными индексами чередуются; недостающие элементы строк заполняются нулями. Отчеркивая соответствующие строки и столбцы таблицы, получим п определителей Гурвица:

Условием устойчивости для систем первого порядка (п = 1) является а0 > 0, а1 >0; второго порядка (n = 2)ао>О, а1>0, а2>0; третьего порядка (п = 3) ао>0, а1>0, а2>0, а1а2>а3а0.
Достоинством критерия устойчивости Payca—Гурвица являются
его сравнительная простота и небольшой объем вычислений при невысоком порядке дифференциального уравнения системы. Для систем более высокого порядка n 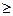 4 использование этого критерия затруднительно ввиду значительного объема вычислений. В таких случаях применяют другие критерии, использующие частотные характеристики АСР.
4 использование этого критерия затруднительно ввиду значительного объема вычислений. В таких случаях применяют другие критерии, использующие частотные характеристики АСР.
Критерий устойчивости Михайлова — это частотный критерий, основанный на построении по характеристическому уравнению системы так называемой характеристической кривой, или годографа, по виду которой судят об устойчивости АСР.
Представим левую часть характеристического уравнения в виде функции от р, т. е. F (р) = аорп + a1pn-1+ . . . +ап-1p' +аn.
Заменив р на j  , получим уравнение комплексного вектора
, получим уравнение комплексного вектора
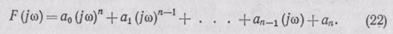
Уравнение (22) можно свести к виду F (j  ) = X (
) = X (  ) + jY (
) + jY (  ), вектор его при изменении
), вектор его при изменении  от 0 до
от 0 до 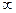 опишет некоторую кривую, называемую годографом Михайлова, по виду которой можно судить об устойчивости системы.
опишет некоторую кривую, называемую годографом Михайлова, по виду которой можно судить об устойчивости системы.
Критерий Михайлова формулируют следующим образом: для устойчивости автоматической системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении  от 0 до
от 0 до 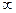 , начиная с положительной вещественной оси, обошел последовательно в положительном направлении (против часовой стрелки) п квадрантов комплексной плоскости.
, начиная с положительной вещественной оси, обошел последовательно в положительном направлении (против часовой стрелки) п квадрантов комплексной плоскости.
На рис. 65, а годографы 1, 2 и 3 характеризуют устойчивые, годограф 5 — неустойчивые системы. Годограф 4 характеризует систему, находящуюся на границе устойчивости. Анализ АСР производят в следующем порядке:
1) в характеристическом уравнении АСР заменяют р на j  ;
;
2) члены с j
