Задачи, приводящие к понятию определенного интеграла

Пусть функция определена на отрезке и неотрицательна, т.е. 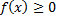при всех 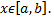Рассмотрим фигуру, ограниченную графиком функции 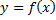и прямыми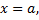

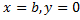
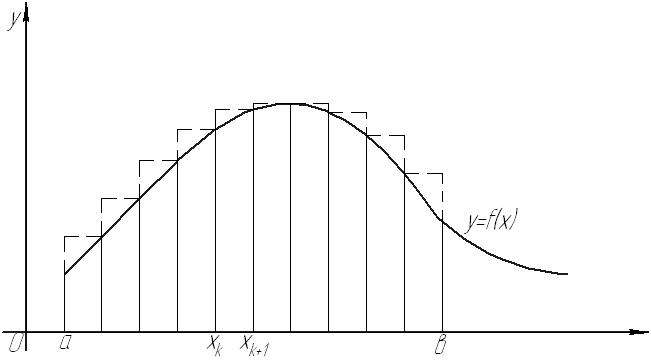
Рис. 37

Криволинейная трапеция

Полученную фигуру называют криволинейной трапецией. Задача состоит в том, чтобы дать определение и указать способ вычисления площади криволинейной трапеции.

Для этого разобьем отрезок на отрезков точками

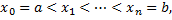
проведем через эти точки прямые, параллельные оси

Таким образом, криволинейная трапеция разобьется на частей, каждая из которых также будет криволинейной трапецией. Пусть

.

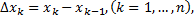
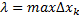В каждом отрезке 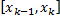выберем произвольную точку .

Рассмотрим ступенчатую фигуру, состоящую из прямоугольников с основаниями и высотами 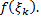Площадь 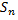этой ступенчатой фигуры вычисляется по формуле

При достаточно малых отрезках 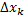ступенчатая фигура будет мало отличаться от исходной криволинейной трапеции. Поэтому за площадь криволинейной трапеции 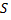принимают предел площадей ступенчатых фигур при стремлении к нулю длин всех отрезков разбиения

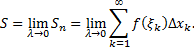
Рассмотрим другую задачу. Пусть материальная точка движется вдоль оси 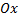из точки в точку 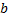под действием силы , направление действия силы совпадает с направлением движения точки и величина силы 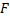задана как функция от координаты точки, т.е.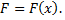

Задача состоит в том, чтобы найти работу силы 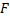при перемещении материальной точки из точки в точку Для этого следует разбить отрезок на частей точками. В каждом отрезке 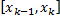произвольно выберем точку

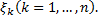
Тогда работа силы 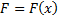на каждом отрезке 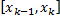приближенно равна 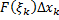, а на всем отрезке работу этой силы можно приближенно считать равной сумме

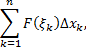
т.е.

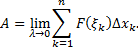
Таким образом, предел этой суммы есть работа переменной силы при перемещении материальной точки из точки в точку