Определение определенного интеграла
Вывод: если существует конечный предел интегральных сумм
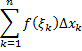
при 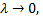 причем этот предел не зависит ни от способа разбиения отрезка
причем этот предел не зависит ни от способа разбиения отрезка  на части, ни от выбора точек
на части, ни от выбора точек 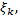 то функция
то функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке  , а указанный предел называется определенным интегралом от функции
, а указанный предел называется определенным интегралом от функции  по отрезку
по отрезку  и обозначается символом
и обозначается символом
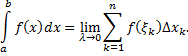
Если выполнено одно из следующих условий:
- функция  непрерывна на отрезке
непрерывна на отрезке  ;
;
- функция  ограничена на отрезке
ограничена на отрезке  и имеет на этом отрезке конечное число точек разрыва;
и имеет на этом отрезке конечное число точек разрыва;
- функция  монотонна на отрезке
монотонна на отрезке  ;
;
то  интегрируема на отрезке
интегрируема на отрезке  и, следовательно, существует
и, следовательно, существует
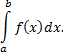
В этом геометрический смысл определенного интеграла.
Кроме того, работа непрерывной на отрезке  переменной силы
переменной силы 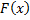 при перемещении материальной точки из точки
при перемещении материальной точки из точки  в точку
в точку  , вычисляется по формуле
, вычисляется по формуле
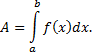
Дата добавления: 2015-08-11; просмотров: 727;
