Понятие линейного оператора. Основные свойства. Собственные числа и собственные векторы. Квадратичные формы.
Цель: Изучить понятия линейного оператора и его собственных чисел и собственных векторов, методы их нахождения.
Определение. Пусть 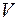 и
и 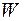 – линейные пространства размерности
– линейные пространства размерности 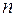 и
и 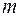 соответственно,
соответственно, 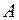 – будем называть оператором, действующим из
– будем называть оператором, действующим из 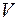 и
и 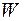
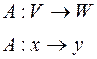 ,
, 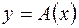 или
или 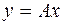 , говорят что y – образ элемента x, а x – прообраз y.
, говорят что y – образ элемента x, а x – прообраз y.
Определение. Оператор 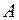 , действующий из
, действующий из 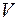 в
в 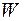 называется линейным, если для
называется линейным, если для 
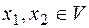 и
и 
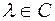 выполняются соотношения:
выполняются соотношения:
1. 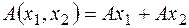 .
.
2. 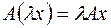 .
.
Если 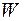 (комплексная плоскость), то
(комплексная плоскость), то 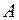 – называют линейным функционалом. Если
– называют линейным функционалом. Если 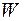 совпадает с
совпадает с 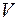 , то
, то 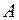 – называют линейным преобразованием пространства.
– называют линейным преобразованием пространства.
Определение.Произведение λ на 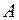 называется оператор λA определяемый равенством
называется оператор λA определяемый равенством 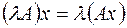 .
. 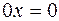 , где
, где 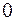 нулевой оператор,
нулевой оператор,
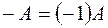 , противоположный
, противоположный 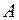 оператор.
оператор. 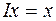 - I – тождественный или единичный оператор.
- I – тождественный или единичный оператор.
Определение.Произведением оператора 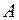 на
на 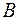 называется оператор, для которого верны следующие соотношения
называется оператор, для которого верны следующие соотношения 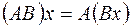 :
:
1) 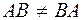 ;
;
2) 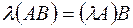 ;
;
3) 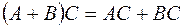 ;
;
4) 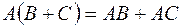 ;
;
5) 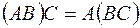 .
.
Определение.Оператор 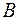 называется обратным для
называется обратным для 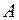 если,
если, 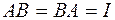 , обозначают
, обозначают 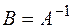 .
.
Определение. Ядром линейного оператора 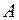 называется множество всех элементов
называется множество всех элементов 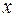 пространства
пространства 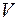 , для которых
, для которых 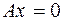 :
: 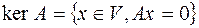 .
.
Определение.Образом линейного оператора 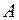 называется множество элементов
называется множество элементов 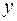 таких что
таких что 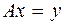 :
: 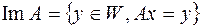 .
.
Определение.Рангом линейного оператора называется число равное 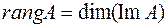 .
.
Теорема. Пусть 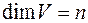 и пусть
и пусть 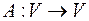 , тогда
, тогда 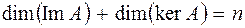 .
.
Дата добавления: 2015-08-26; просмотров: 815;
