Свойство самосопряженного линейного оператора

1. Собственные значения самосопряженного оператора вещественны.

2. Если A – самосопряженный оператор, то собственные векторы, отвечающие различным собственным значениям этого оператора ортогональны.

Определение. Квадратичной формой называется однородный многочлен второй степени относительно n переменных 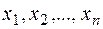. Квадратичную форму всегда можно представить в виде: 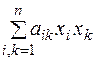, ( 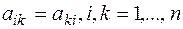), где 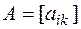- симметрическая матрица (т.е. ).

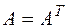Если 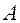– вещественная симметричная матрица, то форма называется вещественной, 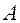– самосопряженная.

В дальнейшем будем рассматривать вещественные квадратичные формы.

Теорема. Для каждой квадратичной формы существует базис, в котором она имеет канонический вид (т.е. представляет сумму квадратов) или такой вид в котором матрица квадратичной формы имеет диагональный вид.