Приведение кривой 2-го порядка к каноническому виду.

Рассмотрим общее уравнение кривой 2-го порядка в евклидовом пространстве, с ортонормированным базисом , ,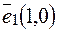

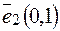1) Выделим квадратичную форму ;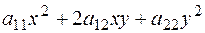

Приведем её к каноническому виду, для этого найдем собственные значения

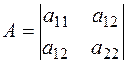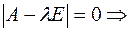
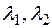, - вещественные числа

следовательно .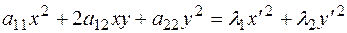

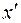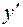2) Для того чтобы выразить x, y через и , найдем координаты векторов нового базиса. За новый базис необходимо взять ортонормированные собственные векторы квадратичной формы соответственно λ₁ и λ₂, для того чтобы их найти необходимо решить системы.

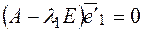и

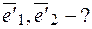Матрица перехода от старых координат к новым координатам имеет вид:

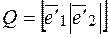, т. е. 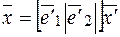, где ,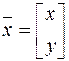

Перейдя к новым координатам и выполнив все элементарные преобразования, получим канонический вид (параллельный перенос) кривой 2-го порядка в собственном базисе оператора квадратичной формы.

Пример. Привести кривую второго порядка к каноническому виду.

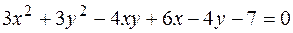
Решение.1)Найдем собственные числа

,

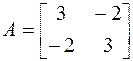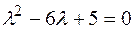
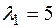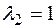, , следовательно

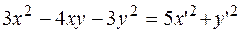
2) Найдем собственные векторы соответствующие собственным значениям и перейдем к новому ортонормированному базису:

а) 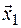, соответствующий. ,

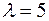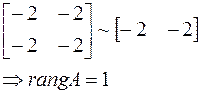
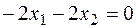
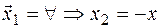
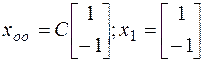
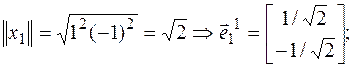
б) 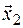, соответствующий. ,

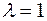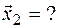
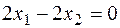
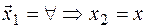
3) Составим матрицу перехода Q:

.

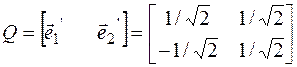Перепишем старые координаты через новые. X=QX’

,

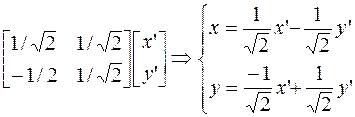Перепишем уравнение кривой второго порядка в новых координатах.

,

,

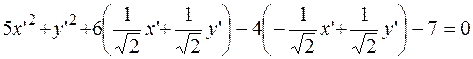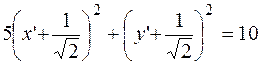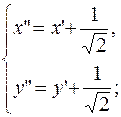выполним параллельный перенос и получим следующее уравнение ,

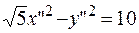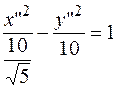- уравнение гиперболы.