Матричная запись линейных операторов.
Фиксируем в линейном пространстве 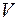 базис
базис 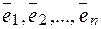 пусть
пусть 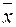 – произвольный элемент
– произвольный элемент 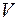 и
и 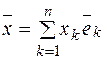 (разложение
(разложение 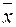 по базису
по базису 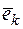 ).
).
Пусть 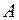 – линейный оператор
– линейный оператор 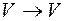 . Тогда имеем
. Тогда имеем 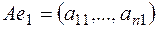 ,
,
…, 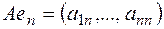 .
. 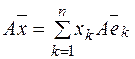 . Пусть
. Пусть 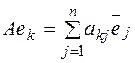 образы базисных векторов, тогда
образы базисных векторов, тогда 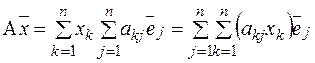 , т. е.
, т. е. 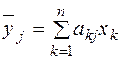 , j=1,…,n,
, j=1,…,n,  .
.
Рассмотрим 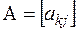 матрицу линейного оператора в заданном базисе
матрицу линейного оператора в заданном базисе 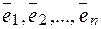 , это матрица столбцами которой являются координаты базисных векторов
, это матрица столбцами которой являются координаты базисных векторов 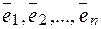 . Причем единственный линейный оператор
. Причем единственный линейный оператор 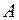 , матрицей которого в заданном базисе
, матрицей которого в заданном базисе 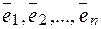 будет матрица
будет матрица 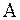 .
.
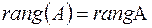 ,
, 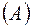 - оператор.
- оператор.
При этом соотношения 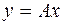 ,
, 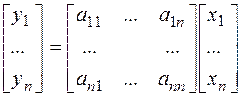 , с одной стороны связывают образ
, с одной стороны связывают образ 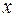 с координатами прообраза
с координатами прообраза 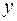 , с другой стороны, описывают действие линейного оператора
, с другой стороны, описывают действие линейного оператора 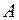 заданного матрицей A. При изменении базиса матрица линейного оператора A также изменится.
заданного матрицей A. При изменении базиса матрица линейного оператора A также изменится.
Пусть задан базис 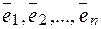 в пространстве
в пространстве 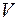 и
и 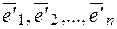 - новый базис, а U – матрица перехода от базиса
- новый базис, а U – матрица перехода от базиса 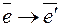 , тогда матрица линейного оператора в двух базисах связаны следующим соотношением:
, тогда матрица линейного оператора в двух базисах связаны следующим соотношением: 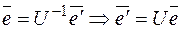 , т. к.
, т. к. 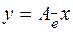
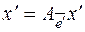 ,
, 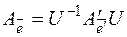 и
и 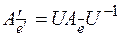
 ,
, 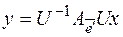 .
.
Определение. Число λ называется собственным значением 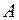 если существует ненулевой вектор
если существует ненулевой вектор 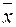 такой, что
такой, что 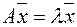 , при этом
, при этом 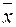 называется собственным вектором оператора
называется собственным вектором оператора 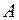 . Т.к.
. Т.к. 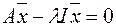 ,
, 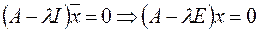 , тогда чтобы однородная система имела ненулевое решение необходимо и достаточно, чтобы
, тогда чтобы однородная система имела ненулевое решение необходимо и достаточно, чтобы 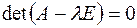 . Многочлен
. Многочлен 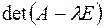 называется характеристическим многочленом
называется характеристическим многочленом 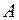 .
.
Чтобы найти собственные числа нужно решить уравнение 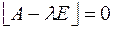 .
.
Чтобы найти собственный вектор 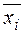 , соответствующий собственному числу
, соответствующий собственному числу 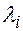 необходимо решить систему
необходимо решить систему 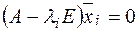 .
.
Дата добавления: 2015-08-26; просмотров: 2005;
