Глава 3. Устойчивость линейных систем
§ 1. Определение и условие устойчивости
Одной из основных динамических характеристик САР является её устойчивость. Под устойчивостью понимается свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, нарушившего равновесие.
Устойчивость системы определяется характером протекания переходного процесса, возникающего при нарушении равновесия каким-либо возмущающим воздействием. Переходный процесс, представляющий собой закон изменения регулируемой величины y(t) во времени, зависит как от свойств системы, так и от вида возмущения.
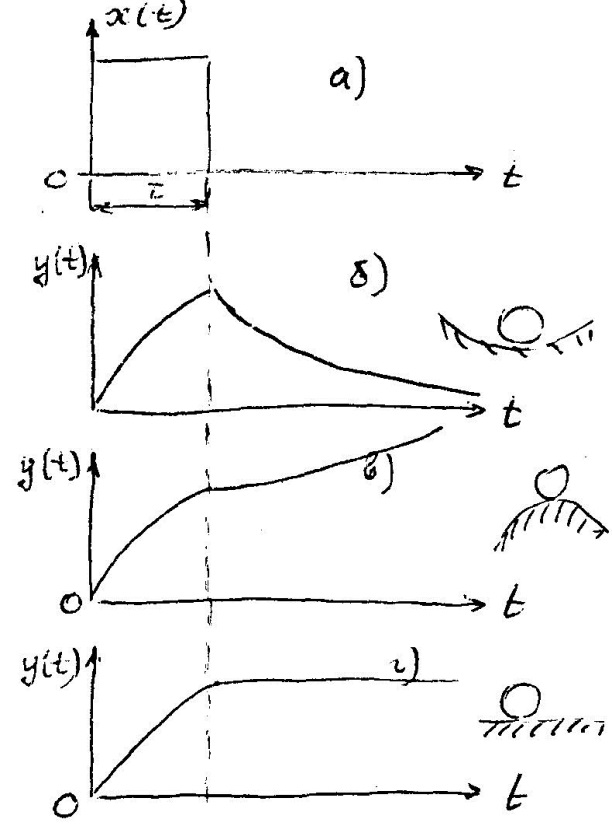
Условие устойчивости определяет три основных вида движения системы: движение устойчивой системы (рис. 1б), движение неустойчивой системы (рис. 1в) и движение нейтральной системы (системы, находящейся на границе устойчивости) (рис. 1г). Рисунок 1 показывает, что устойчивость системы определяется характером её движения после прекращения действия входного воздействия (при t > τ).
Рисунок 1
В случае устойчивой системы переходный процесс со временем затухает, и система вновь возвращается в устойчивое состояние. Таким образом, устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими. Для неустойчивых систем характерен процесс ухода от установившегося состояния.
Приведённые понятия устойчивости определяют устойчивость установившегося режима системы. Однако, система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим вообще отсутствует. С учётом этих условий работы можно дать следующее, более общее определение устойчивости: система устойчива, если её выходная величина остаётся ограниченной в условиях действия на систему ограниченных по величине возмущений.
Определим, от чего зависит устойчивость САР. Для этого рассмотрим уравнение динамики системы, которое в общем случае имеет вид:
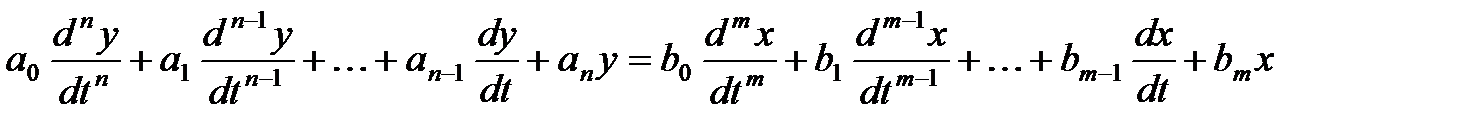 . (1)
. (1)
Характер переходных процессов в системе определяется видом левой части дифференциального уравнения (1).
Уравнение (1) является неоднородным дифференциальным уравнением, так как его правая часть не равна нулю.
Процесс регулирования определяется решением дифференциального уравнения как сумма двух решений:
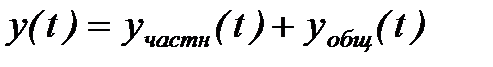 , (2)
, (2)
где 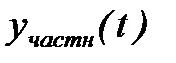 - частное решение неоднородного уравнения (1) с правой частью;
- частное решение неоднородного уравнения (1) с правой частью;
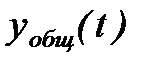 - общее решение уравнения (1) без правой части, т.е. с правой частью, равной нулю.
- общее решение уравнения (1) без правой части, т.е. с правой частью, равной нулю.
В случае 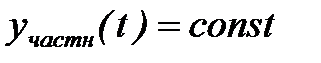 это будет установившееся значение
это будет установившееся значение 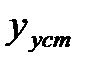 . Первое слагаемое в (2) называют также вынужденной составляющей
. Первое слагаемое в (2) называют также вынужденной составляющей 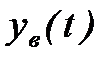 , а второе слагаемое – свободной (переходной) составляющей
, а второе слагаемое – свободной (переходной) составляющей 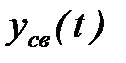 , т.к. оно характеризует движение системы при отсутствии внешнего воздействия. Тогда формула (2) может быть записана в виде
, т.к. оно характеризует движение системы при отсутствии внешнего воздействия. Тогда формула (2) может быть записана в виде
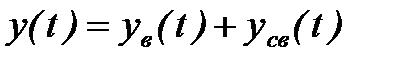 .
.
САР будет устойчивой, если с течением времени при 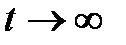 свободная составляющая будет стремиться к нулю
свободная составляющая будет стремиться к нулю
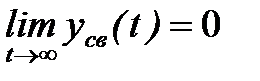 . (3)
. (3)
Выражение (3) определяет основное условие устойчивости системы. Найдём свободную составляющую из уравнения (1). Для этого необходимо решить однородное дифференциальное уравнение
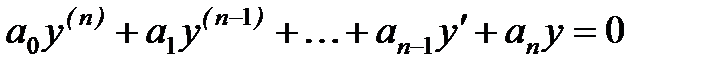 . (4)
. (4)
Тогда характеристическое уравнение, соответствующее (4), имеет вид
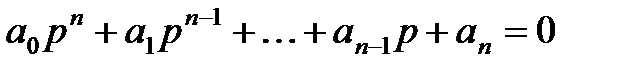 , (5)
, (5)
где p – комплексное число, которое является решением (корнем) характеристического уравнения.
Общее решение однородного дифференциального уравнения имеет вид
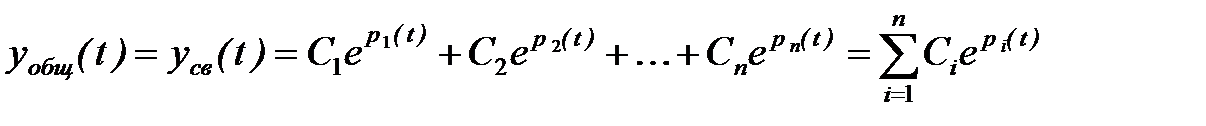 , (6)
, (6)
где 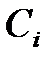 - постоянные интегрирования, определяемые параметрами системы и начальными условиями;
- постоянные интегрирования, определяемые параметрами системы и начальными условиями;
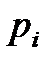 - корни характеристического уравнения.
- корни характеристического уравнения.
Так как в понятие устойчивости системы входит только факт наличия или отсутствия затухания переходного процесса, то устойчивость линейной САР не зависит от вида правой части дифференциального уравнения (1) и определяется только характеристическим уравнением (5).
Определим, какие свойства корней характеристического уравнения необходимы и достаточны для того, чтобы САР была устойчивой.
Корни могут быть вещественными, комплексными и чисто мнимыми.
Рассмотрим эти случаи.
1. Вещественный корень.
Пусть один из корней, например 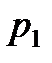 , является вещественным. Если он отрицательный
, является вещественным. Если он отрицательный 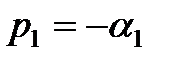 , то ему в (6) будет соответствовать слагаемое
, то ему в (6) будет соответствовать слагаемое 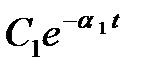 , которое при
, которое при 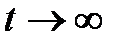 представляет собой затухающую экспоненту.
представляет собой затухающую экспоненту.
При 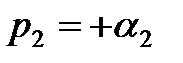 получается расходящийся процесс.
получается расходящийся процесс.
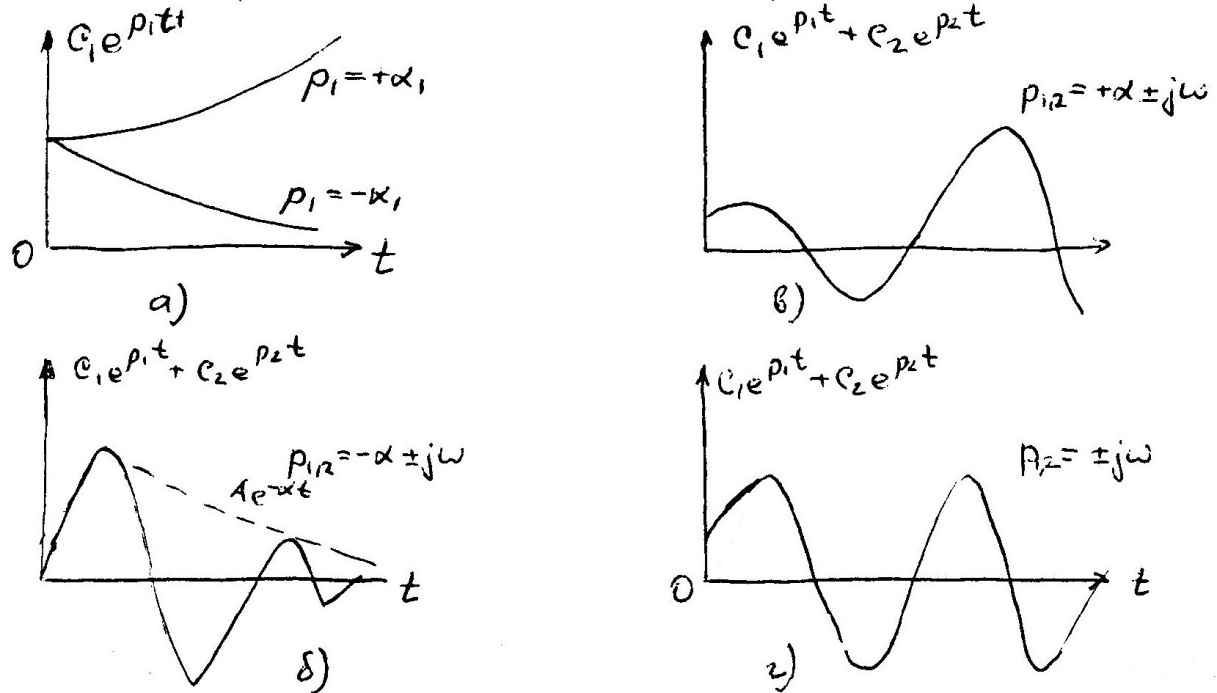
 Рисунок 2
Рисунок 2
2. Комплексные корни.
Комплексные корни всегда получаются попарно сопряжёнными. При отрицательной вещественной части два корня, например p1 и p2 будут иметь вид 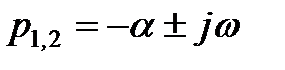 . В этом случае слагаемые, определяемые этими корнями в уравнении (6), могут быть представлены в виде
. В этом случае слагаемые, определяемые этими корнями в уравнении (6), могут быть представлены в виде
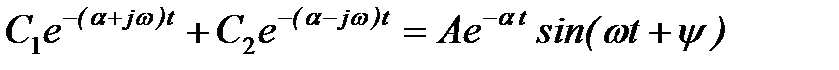 ,
,
где А и 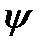 - новые постоянные интегрирования,
- новые постоянные интегрирования,
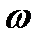 - угловая частота колебаний,
- угловая частота колебаний,
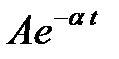 - амплитуда колебаний,
- амплитуда колебаний,
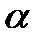 - коэффициент затухания.
- коэффициент затухания.
Очевидно, что в этом случае получаются затухающие колебания (рис. 2б).
В случае 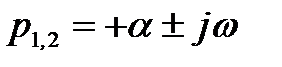 колебания будут расходящимися (рис. 2в).
колебания будут расходящимися (рис. 2в).
3. Чисто мнимые корни.
В этом случае 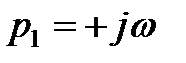 и
и  . Слагаемое, определяемое этими корнями в (6), будет представлять собой незатухающие колебания, т.е. колебания с постоянной амплитудой
. Слагаемое, определяемое этими корнями в (6), будет представлять собой незатухающие колебания, т.е. колебания с постоянной амплитудой
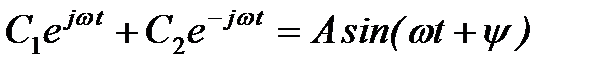 .
.
Такой процесс изображён на рис. 2г.
Следовательно, для затухания переходного процесса необходимо, чтобы вещественные корни и вещественные части комплексных корней характеристического уравнения были бы отрицательными, так как
 .
.
Если хотя бы один корень будет иметь положительную вещественную часть, то он даёт расходящуюся составляющую переходного процесса и САР будет неустойчивой. Таким образом, необходимым и достаточным условием устойчивости САР являются отрицательность вещественных частей всех корней её характеристического уравнения.
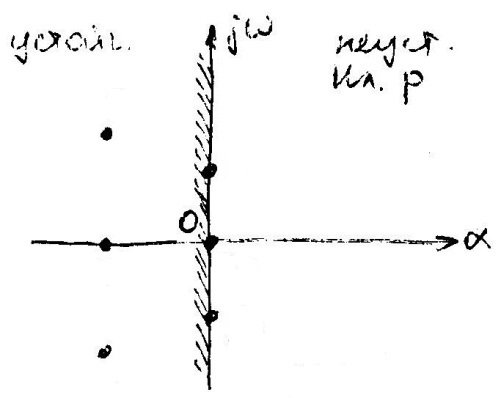
Корни характеристического уравнения можно представить в виде точек на комплексной плоскости корней (рис. 3).
| p5 |
| p6 |
| p4 |
| p3 |
| p2 |
| p1 |
| Рисунок 3 |
Корни p1 и p2 – комплексно-сопряжённые
p3 – вещественный
p4 – нулевой
p5 и p6 – чисто мнимые
В связи с этим условие устойчивости системы можно сформулировать следующим образом: система будет устойчивой, если все корни характеристического уравнения этой системы будут располагаться в левой полуплоскости (левые корни) и неустойчивой, если хотя бы один корень находится в правой полуплоскости (правый корень).
Таким образом, мнимая ось комплексной плоскости представляет собой границу устойчивости системы. Система будет находиться на границе устойчивости при наличии:
1) нулевого корня (p4);
2) пары чисто мнимых корней ( p5 и p6).
В обоих случаях предполагается, что все остальные корни лежат в левой полуплоскости.
В первом случае корень попадает в начало координат. Это значит, что в характеристическом уравнении (5) свободный член 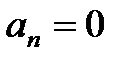 . Дифференциальное уравнение (1) в этом случае может быть записано в виде
. Дифференциальное уравнение (1) в этом случае может быть записано в виде

и САР будет устойчивой не относительно регулируемой величины 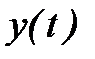 , а относительно её скорости изменения
, а относительно её скорости изменения 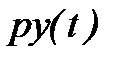 . Величина же регулируемой величины может принимать произвольные значения. Такую систему называют нейтрально-устойчивой, имея в виду её безразличие к значению самой регулируемой величины.
. Величина же регулируемой величины может принимать произвольные значения. Такую систему называют нейтрально-устойчивой, имея в виду её безразличие к значению самой регулируемой величины.
На границе устойчивости второго типа, которая называется колебательной границей устойчивости, два корня попадают на ось мнимых. В этом случае САР будет иметь незатухающие колебания с постоянной амплитудой (рис. 2г).
Покажем, что необходимым (но не достаточным) условием устойчивости системы является положительность всех коэффициентов характеристического уравнения. Действительно, если известны все корни характеристического уравнения p1, p2,…, pn, то оно может быть представлено в виде
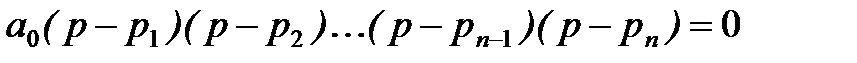 , где
, где 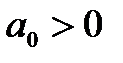 (7)
(7)
В устойчивой системе все вещественные корни 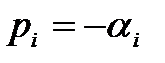 , а все комплексные корни
, а все комплексные корни 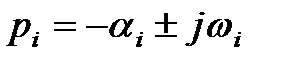 .
.
Тогда уравнение (7) при подстановке значений корней можно записать так
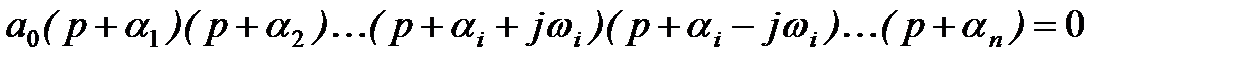
или
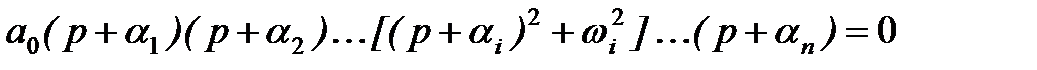 .
.
Очевидно, что при раскрытии скобок в этом уравнении все коэффициенты характеристического уравнения должны быть положительны, так как перемножая и складывая положительные величины 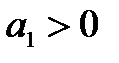 ,
, 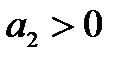 и т.д. нельзя получить отрицательные величины. Таким образом, если в характеристическом уравнении хотя бы один коэффициент отрицателен или равен нулю, то система неустойчива.
и т.д. нельзя получить отрицательные величины. Таким образом, если в характеристическом уравнении хотя бы один коэффициент отрицателен или равен нулю, то система неустойчива.
Необходимое условие устойчивости является достаточным для уравнений первого и второго порядков, в чём легко убедиться непосредственно.
§ 2. Критерии устойчивости
Практически для определения устойчивости необязательно знать численные значения корней характеристического уравнения. Достаточно убедиться только в отрицательности вещественных частей корней. Поэтому целесообразно воспользоваться более простым методом определения устойчивости, основанном на выявлении отрицательности вещественных частей корней (без нахождения их значений). Такие методы основываются на использовании критериев устойчивости и выделении областей устойчивости. Рассмотрим эти критерии.
1. Критерий Рауса-Гурвица
Этот критерий относится к алгебраическим критериям, накладывающим ограничения на коэффициенты характеристического уравнения.
Этот критерий был предложен английским математиком Раусом в 1845 г., а затем вновь выведен и дополнен Гурвицем в 1893 г.
Рассмотрим этот критерий в форме Гурвица.
Пусть характеристическое уравнение системы имеет вид
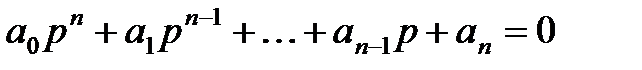 , причём
, причём 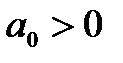 (1)
(1)
Тогда для устойчивости линейной САР необходимо и достаточно, чтобы были положительными главный определитель Гурвица и все его дислокальные миноры, т.е. при 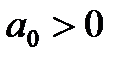
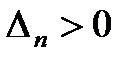 ;
; 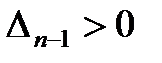 ; …;
; …; 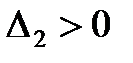 ;
; 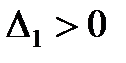 .
.
Диагональные миноры (определители Гурвица) представляют собой диагональные определители квадратной матрицы Гурвица n-го порядка
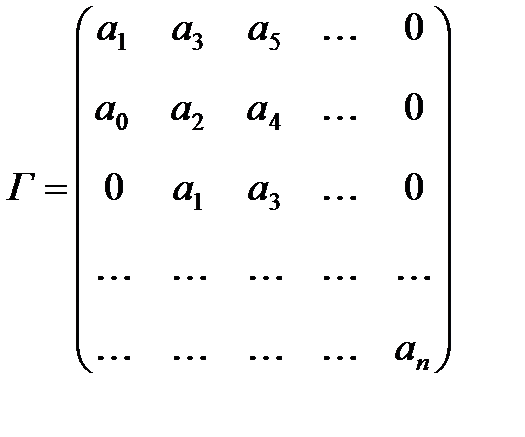 , (2)
, (2)
составленной из коэффициентов уравнения (1). При этом
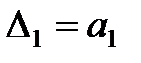 ,
, 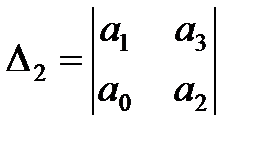 ,
, 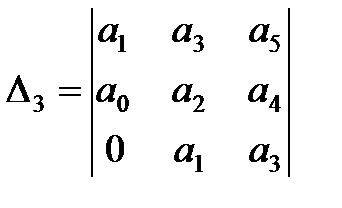 , …,
, …,  .
.
Матрица Гурвица составляется следующим образом. По главной диагонали выписываются все коэффициенты по порядку от 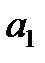 до
до 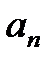 . В каждом столбце вверх от коэффициента главной диагонали записывают коэффициенты с последовательно возрастающими индексами, а вниз – с убывающими. В случае равенства какого-либо коэффициента нулю, а также если индекс его меньше нуля или больше n, в матрице на его место записывается ноль.
. В каждом столбце вверх от коэффициента главной диагонали записывают коэффициенты с последовательно возрастающими индексами, а вниз – с убывающими. В случае равенства какого-либо коэффициента нулю, а также если индекс его меньше нуля или больше n, в матрице на его место записывается ноль.
Из матрицы (2) следует, что главный определитель Гурвица можно записать

Если 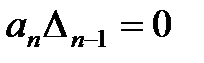 , то система находится на границе устойчивости. При этом возможны два случая:
, то система находится на границе устойчивости. При этом возможны два случая: 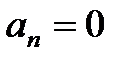 или
или 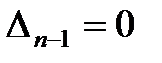 . В первом случае система будет находиться на апериодической границе устойчивости, поскольку один из корней характеристического уравнения равен нулю (см. § 1). Во втором случае система будет находиться на колебательной границе устойчивости, т.к. два комплексно-сопряжённых корня характеристического уравнения находятся на мнимой оси комплексной плоскости корней.
. В первом случае система будет находиться на апериодической границе устойчивости, поскольку один из корней характеристического уравнения равен нулю (см. § 1). Во втором случае система будет находиться на колебательной границе устойчивости, т.к. два комплексно-сопряжённых корня характеристического уравнения находятся на мнимой оси комплексной плоскости корней.
Следует отметить, что из условия 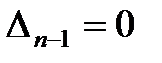 можно определить критическое значение коэффициента усиления Ккр (или другого параметра), при котором система находится на границе устойчивости.
можно определить критическое значение коэффициента усиления Ккр (или другого параметра), при котором система находится на границе устойчивости.
Критерий Рауса-Гурвица целесообразно использовать для уравнений не выше четвёртой-пятой степени. В этих случаях условия устойчивости имеют следующий вид:
1. Для уравнения первого порядка (n=1)
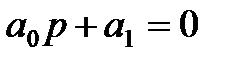 .
.
Условия устойчивости:
 ,
,  .
.
2. Для уравнения второго порядка (n=2)
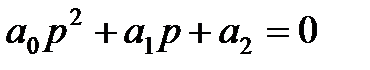
Условия устойчивости:
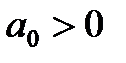 ,
, 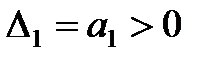 ,
, 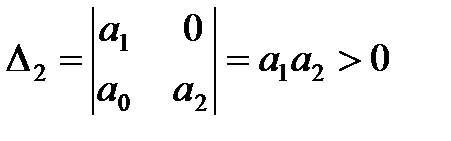
или 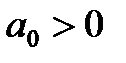 ,
,  ,
, 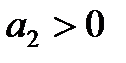 .
.
Таким образом, для уравнений первого и второго порядков необходимым и достаточным условием является только положительность всех коэффициентов характеристического уравнения.
3. Для уравнения третьего порядка (n=3)
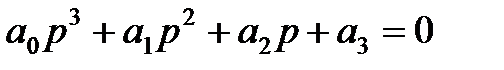
Условия устойчивости:
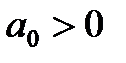 ,
,
 ,
,
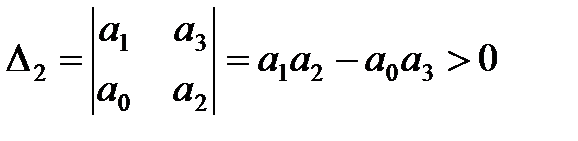 или
или 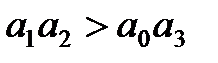 ,
,
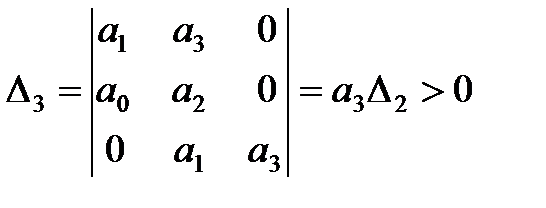 , т.е.
, т.е.  .
.
Следовательно, в этом случае САР будет устойчивой, если
1) 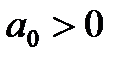 ,
, 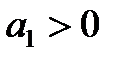 ,
, 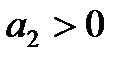 ,
, 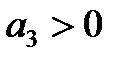 ,
,
2) 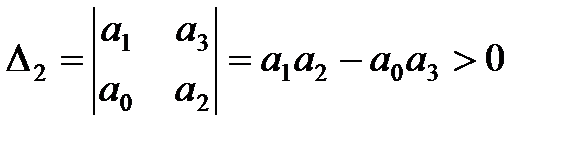 .
.
4. Для уравнения четвёртой степени (n=4)
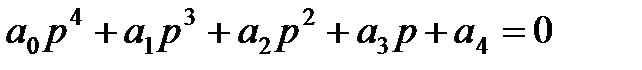
Условия устойчивости:
1) 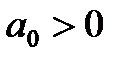 ,
, 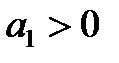 ,
, 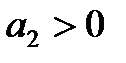 ,
, 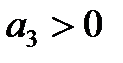 ,
, 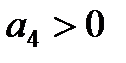 ,
,
2) 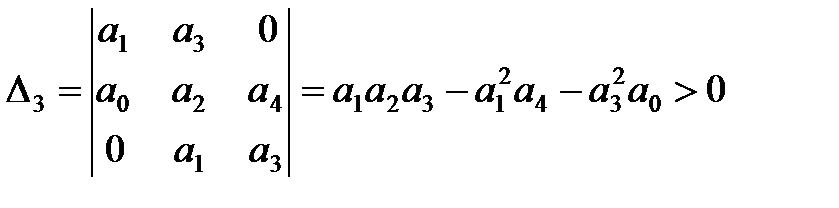 .
.
Таким образом, для уравнений третьего и четвёртого порядков должны быть положительными кроме всех коэффициентов предпоследние определители Гурвица.
2. Критерий устойчивости Михайлова
Этот критерий принадлежит к числу частотных критериев и позволяет судить об устойчивости замкнутой системы по виду годографа, построенного с помощью характеристического уравнения.
Передаточная функция замкнутой системы
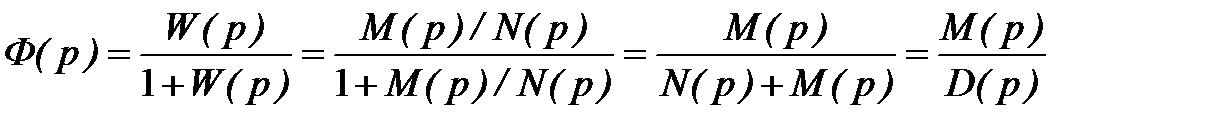 ,
,
где 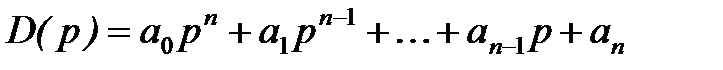 - (3)
- (3)
характеристический полином замкнутой системы.
В уравнении (3) произведём замену 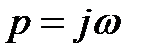 . В результате получим функцию комплексного переменного, представляющую собой характеристический вектор
. В результате получим функцию комплексного переменного, представляющую собой характеристический вектор
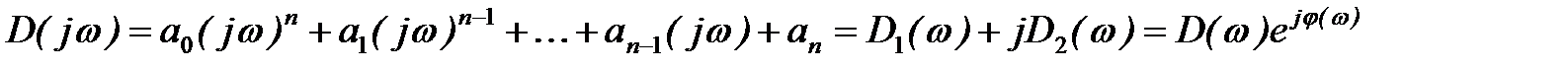 ,
,
где 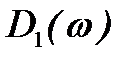 и
и 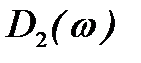 - вещественная и мнимая части комплексной функции:
- вещественная и мнимая части комплексной функции:
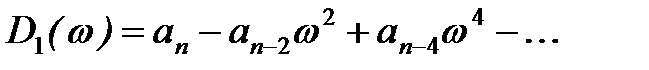 ,
,
 ;
;
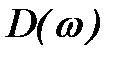 и
и 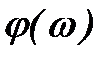 - модуль и фаза (аргумент) комплексной функции.
- модуль и фаза (аргумент) комплексной функции.
Если изменять значение частоты 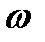 от 0 до
от 0 до 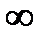 , то вектор
, то вектор 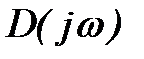 будет изменяться как по величине, так и направлению и вычертит своим концом кривую (годограф), которая называется кривой Михайлова.
будет изменяться как по величине, так и направлению и вычертит своим концом кривую (годограф), которая называется кривой Михайлова.
Выясним связь между видом кривой Михайлова и корнями характеристического уравнения. Для этого определим, чему должен равняться угол поворота φ вектора 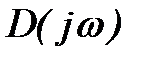 при изменении
при изменении 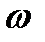 от 0 до
от 0 до 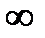 .
.
Запишем характеристический полином в виде произведения сомножителей
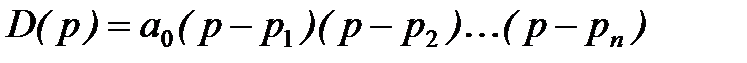 ,
,
где 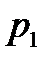 ,
, 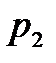 , …,
, …,  - корни характеристического уравнения.
- корни характеристического уравнения.
Аналогично характеристический вектор можно представить в виде
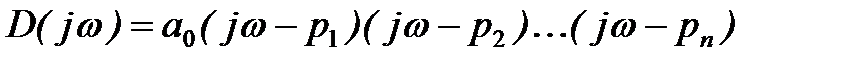
или
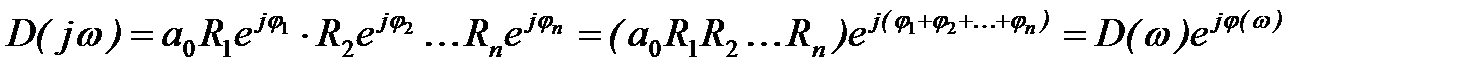 , (4)
, (4)
где 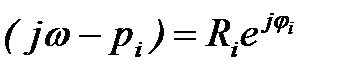 - комплексное число,
- комплексное число, 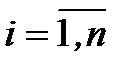 .
.
На плоскости комплексного переменного величина 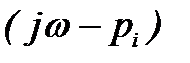 представляет собой вектор, т.к. является разностью векторов ОВ и ОА, модули которых равны
представляет собой вектор, т.к. является разностью векторов ОВ и ОА, модули которых равны 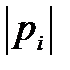 и
и 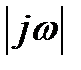 (рис. 4).
(рис. 4).
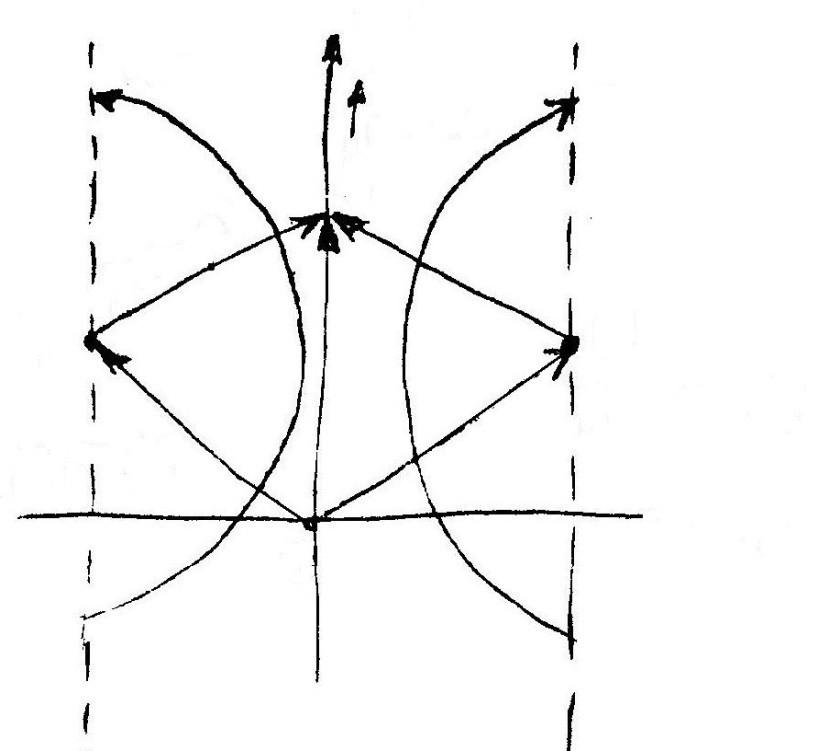
| А |
| В |
| О |
| С |
| α |
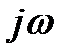
|
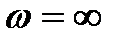
|
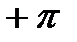
|
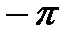
|
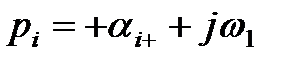
|
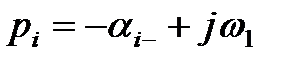
|
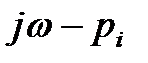
|
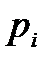 (точка А неподвижна) конец вектора
(точка А неподвижна) конец вектора 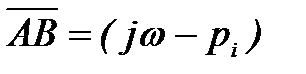 будет скользить вдоль мнимой оси и повернётся в положительном направлении (против часовой стрелки) на угол
будет скользить вдоль мнимой оси и повернётся в положительном направлении (против часовой стрелки) на угол 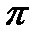 , если корень
, если корень 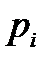 лежит в левой полуплоскости. Если корень
лежит в левой полуплоскости. Если корень 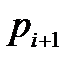 лежит в правой полуплоскости, то поворот вектора
лежит в правой полуплоскости, то поворот вектора 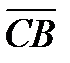 будет совершаться в отрицательном направлении (по часовой стрелке) и составит
будет совершаться в отрицательном направлении (по часовой стрелке) и составит  .
.
Рисунок 4
Из (4) следует, что аргумент вектора 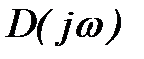 равен сумме аргументов векторов сомножителей
равен сумме аргументов векторов сомножителей 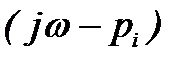
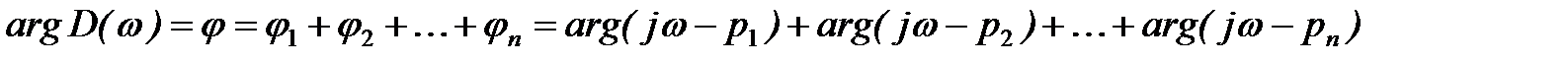
Если предположить, что в правой полуплоскости расположено k корней характеристического уравнения, то в левой полуплоскости их будет (n-k). Тогда изменение аргумента вектора 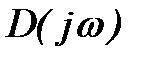 при изменении частоты ω от -∞ до ∞ определится как
при изменении частоты ω от -∞ до ∞ определится как
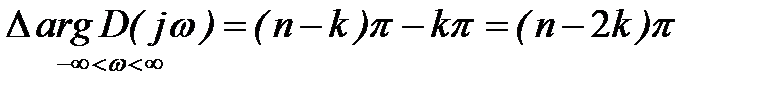 . (5)
. (5)
Формула (5) определяет изменение аргумента вектора 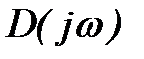 в неустойчивой системе.
в неустойчивой системе.
Диапазон отрицательных частот 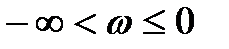 из выражения (5) можно исключить, так как годограф вектора
из выражения (5) можно исключить, так как годограф вектора 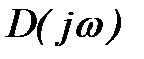 для положительных частот и годограф
для положительных частот и годограф 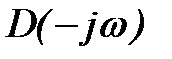 для отрицательных частот относительно действительной оси расположены симметрично. Исключение отрицательного диапазона частот уменьшает изменение аргумента вектора
для отрицательных частот относительно действительной оси расположены симметрично. Исключение отрицательного диапазона частот уменьшает изменение аргумента вектора 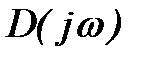 в два раза. Таким образом, формула (5) может быть записана в виде
в два раза. Таким образом, формула (5) может быть записана в виде
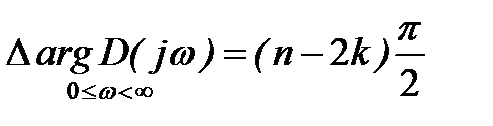 (6)
(6)
Если все корни характеристического уравнения лежат в левой полуплоскости (система устойчива), то k=0 и следовательно
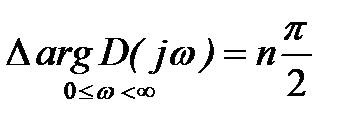 (7)
(7)
Формула (7) определяет необходимые и достаточные условия устойчивости системы в замкнутом состоянии и одновременно являются математической формулировкой критерия устойчивости Михайлова: для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы вектор 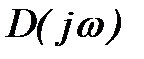 , описывающий своим концом кривую Михайлова, при изменении частоты ω от 0 до ∞, начав своё движение с положительной действительной оси и вращаясь против часовой стрелки, последовательно проходил n квадрантов, нигде не обращаясь в нуль.
, описывающий своим концом кривую Михайлова, при изменении частоты ω от 0 до ∞, начав своё движение с положительной действительной оси и вращаясь против часовой стрелки, последовательно проходил n квадрантов, нигде не обращаясь в нуль.
На рис. 5а приведены типичные кривые (годографы) Михайлова для устойчивых систем, описываемых уравнениями от первого (n=1) до пятого (n=5) порядков. Для удобства сравнения коэффициенты 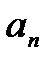 характеристического уравнения во всех случаях приняты одинаковыми.
характеристического уравнения во всех случаях приняты одинаковыми.
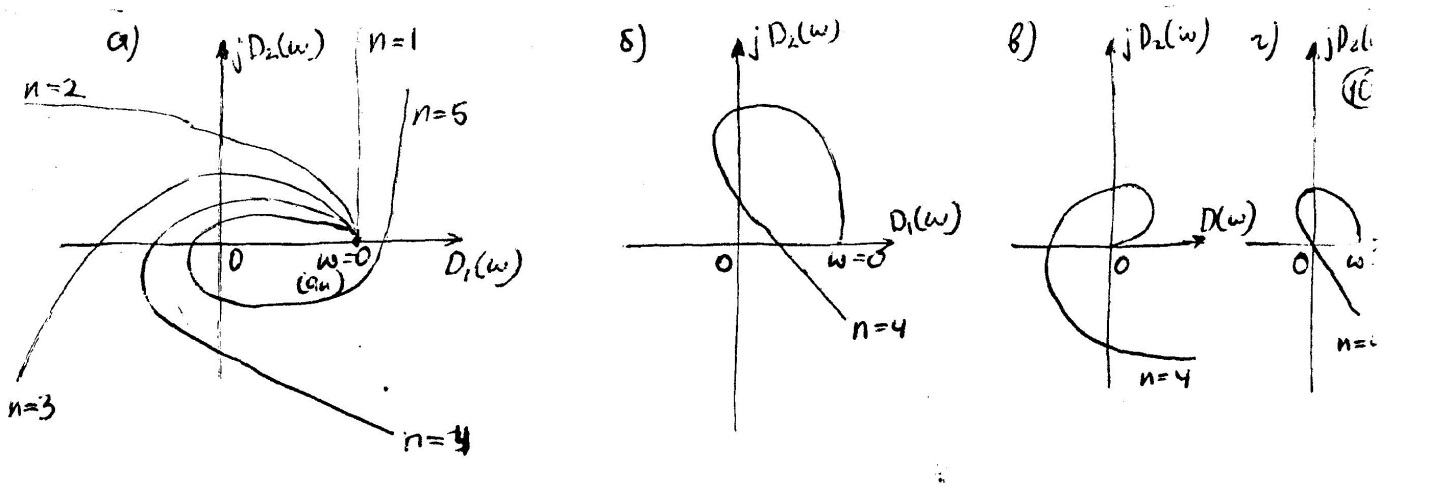
Рисунок 5
Если условия устойчивости по Михайлову не выполняются, то система будет неустойчивой (рис. 5б).
Система будет находиться на границе: апериодической устойчивости (рис. 5в), когда имеется нулевой корень, и годограф Михайлова начинает своё движение из начала координат; колебательной устойчивости (рис. 5г), если имеются сопряжённые мнимые корни, и годограф Михайлова проходит при частотах, отличных от нуля, через начало координат.
Если система при расчёте окажется неустойчивой, то, используя уравнение (6), можно определить количество корней характеристического уравнения  , расположенных в правой полуплоскости комплексной плоскости корней, по формуле:
, расположенных в правой полуплоскости комплексной плоскости корней, по формуле:
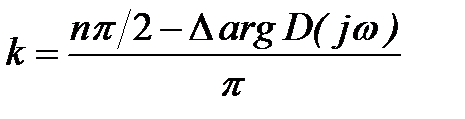
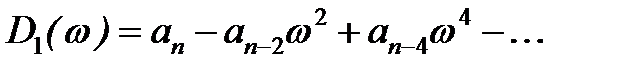
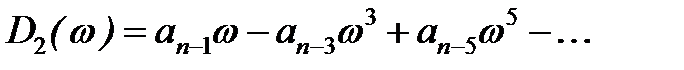
| <== предыдущая лекция | | | следующая лекция ==> |
| Художественные системы в проектировании одежды | | | Конструктивные решения полов малоэтажных зданий |
Дата добавления: 2015-08-11; просмотров: 6740;
