Свойства собственных значений и собственных чисел.
1. Каждый линейный оператор имеет собственное значение.
2. Собственные числа и векторы не всегда вещественные.
3. У симметричной матрицы собственные числа всегда вещественны.
4. Собственные векторы соответствующие собственным значениям различные линейно независимы.
5. Если характеристический многочлен n-ой степени оператора 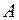 имеет n – различных корней, то в некотором базисе матрица оператора A имеет диагональный вид.
имеет n – различных корней, то в некотором базисе матрица оператора A имеет диагональный вид.
6. Для того чтобы матрица A линейного оператора 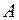 в данном базисе
в данном базисе 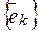 была диагональной, необходимо и достаточно, чтобы базисные векторы
была диагональной, необходимо и достаточно, чтобы базисные векторы 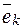 были собственными векторами этого оператора.
были собственными векторами этого оператора.
Определение. Линейный оператор 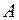 называется самосопряженным, если для любых
называется самосопряженным, если для любых 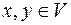 выполняется равенство:
выполняется равенство: 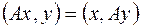 .
.
Дата добавления: 2015-08-26; просмотров: 734;
