Внутренняя энергия и ее основное свойство.

Термодинамика. Лекция 2.

К.т.н. Прохоренко Н.Н.

Расчет основных термодинамических величин ΔU, Q, W.

В предыдущей лекции первый закон термодинамики, будучи специализированной формой записи закона сохранения энергии, был записан в виде:

du = Tds – pdv (2.1)

Здесь приращение внутренней энергии выражено через параметры состояния рабочего тела: термические T и s и деформационные р и v. Первое слагаемое в (2.1) справа представляет собой количество термического взаимодействия между внешней средой и рабочим телом dq = Tds, т.е. количество теплоты, подведенной (отведенной) к рабочему телу. Второе – количество деформационного взаимодействия между внешней средой и системой, т.е. работу сжатия (расширения) dw = pdv. Поэтому иногда удобно записывать первый закон термодинамики (2.1) в виде:

du = dq – dw, (2.2)

где слева характеристика энергии системы, а справа – количества воздействий внешней среды на систему.

В основном уравнении термодинамики (2.2) фигурируют три величины. Чтобы это уравнение стало расчетным инструментом термодинамики, необходимо дать правила независимого расчета по крайней мере двух величин из трех, входящих в (2.2). Начнем с анализа функции u(s,v).

Термодинамические характеристические функции

(функции состояния).

Внутренняя энергия и ее основное свойство.

Рассмотрим интеграл по замкнутому контуру (циклу) от основного уравнения (2.2)

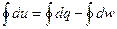
и обратимся к рисунку (2.1).

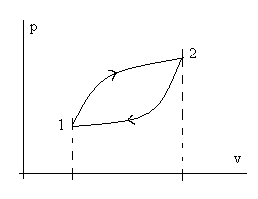
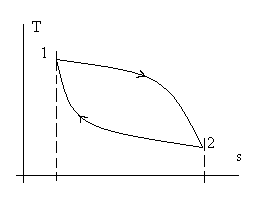
Рис. 2.1. Иллюстрация к пояснению полноты дифференциала du.

Пусть процесс начинается в состоянии (точке) 1, доходит до состояния (точки) 2 и завершается снова в точке 1. Из определения понятия уравнения состояния следует, что

T = T(s,v) и p = p(s,v).

Эти же аргументы относятся к функции (см. (2.1)) u = u(s,v), т.е. u(∙) зависит только от координат (параметров) состояния s и v термодинамической системы, и это естественно с физической точки зрения – ее возврат в исходное состояние (точка 1), где внутренняя энергия имеет только одно определенное значение. Следовательно, для замкнутых (круговых) процессов – в термодинамике они названы циклами:

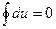(2.3)

Поэтому из математического анализа (из теории функций многих переменных) следует, что du –полный дифференциали изменение функции Δu влюбом процессе 1 - 2

u₂ –u₁ = 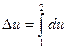(2.4)

или в графической форме - при переходе от точки 1 к точке 2 - не зависит от траектории процесса перехода из точки в точку (см. рис 2.2), а в действительных явлениях характер процесса не влияет на изменение внутренней энергии – оно определяется только состоянием (параметрами) в начале и конце процесса.

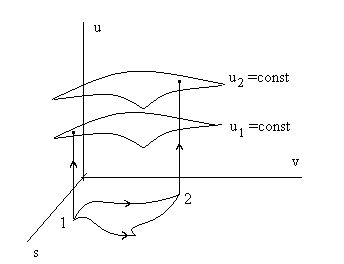
Рис. 2.2. Изменение внутренней энергии u(s,v) не зависит

от траектории F(s,v) = 0 перехода из точки 1 в точку 2.

Определение.Величины (функции), изменение которых не зависят от характера процесса, а определяются только состояниями (параметрами) начала и конца процесса, называются функциями состояния.