Матричный метод решения СЛАУ.
Если определитель основной матрицы системы отличен от нуля, то ее решение определяется формулой:
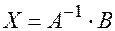 (15.3)
(15.3)
Где 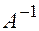 - обратная к основной матрице системы, вычисляемая по формуле
- обратная к основной матрице системы, вычисляемая по формуле 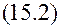 .
.
Совместность однородной и неоднородной СЛАУ.
Рассмотрим однородную СЛАУ

система всегда имеет хотя бы одно решение, например, тривиальное решение 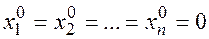 .
.
Когда однородная СЛАУ имеет решения отличные от нулевого?
Заметим, что существует нетривиальное решение ~ линейной зависимости столбцов матрицы однородной СЛАУ (по определению линейной зависимости это означает существует 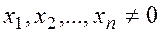 что является уравнениями системы), но по теореме о базисном миноре линейная зависимость имеет место тогда и только тогда когда порядок
что является уравнениями системы), но по теореме о базисном миноре линейная зависимость имеет место тогда и только тогда когда порядок 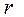 базисного минора меньше числа
базисного минора меньше числа 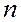 её столбцов. Отсюда теорема.
её столбцов. Отсюда теорема.
Теорема. Однородная СЛАУ имеет нетривиальное решение тогда и только тогда, когда ранг  матрицы системы меньше числа
матрицы системы меньше числа 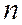 её столбцов.
её столбцов.
Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы этой системы равен нулю.
Решение СЛАУ размерности 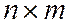
Рассмотрим однородную СЛАУ:
 (15.4)
(15.4)
Данная система всегда имеет хотя бы одно решение, например тривиальное 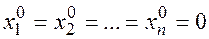 .
.
Теорема: Однородная СЛАУ имеет нетривиальное решение тогда и только тогда, когда ранг 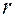 основной матрицы системы меньше числа
основной матрицы системы меньше числа  её неизвестных.
её неизвестных.
Следствие: Квадратная однородная СЛАУ имеет нетривиальное решение тогда и только тогда, когда определитель основной матрицы этой системы равен нулю 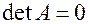 .
.
Если ранг матрицы однородной системы равен 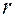 , то система имеет
, то система имеет 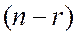 линейно независимых решений:
линейно независимых решений: 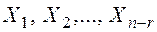 , называемых фундаментальной системой решений.
, называемых фундаментальной системой решений.
Решения 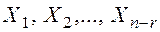 являются линейно независимыми, если ранг матрицы составленной из координатных строк этих векторов равен
являются линейно независимыми, если ранг матрицы составленной из координатных строк этих векторов равен 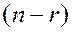 числу этих решений.
числу этих решений.
Теорема: (о структуре решений однородных СЛАУ). Пусть 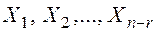 произвольная фундаментальная система решений однородной системы линейных уравнений. Тогда любое решение системы представляет собой линейную комбинацию решений:
произвольная фундаментальная система решений однородной системы линейных уравнений. Тогда любое решение системы представляет собой линейную комбинацию решений:
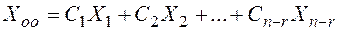 (15.5)
(15.5)
Здесь 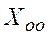 общее решение однородной системы,
общее решение однородной системы, 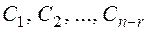 - произвольные постоянные, а
- произвольные постоянные, а  фундаментальная система решений, (частные решения однородной системы), найденная при условии, что свободные неизвестные
фундаментальная система решений, (частные решения однородной системы), найденная при условии, что свободные неизвестные 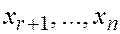 по очереди приравниваются
по очереди приравниваются 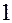 , а остальные при этом равны
, а остальные при этом равны 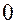 . Неизвестные
. Неизвестные 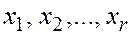 называются базисными неизвестными.
называются базисными неизвестными.
Решение неоднородной системы в общем случае определяется следующей теоремой:
Теорема: (о структуре решения неоднородной СЛАУ): Общее решение неоднородной СЛАУ определяется формулой:
 (15.6)
(15.6)
где 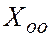 - общее решение соответствующей однородной системы, а
- общее решение соответствующей однородной системы, а  - частное решение неоднородной системы.
- частное решение неоднородной системы.
Для более простого нахождения частного решения, удобно взять свободные неизвестные равными нулю.
Дата добавления: 2015-08-26; просмотров: 1926;
