Системы линейных алгебраических уравнений (СЛАУ).

Цель: Изучить основные понятия СЛАУ, методы определения количества решений и нахождения последних.

Систему уравнений вида

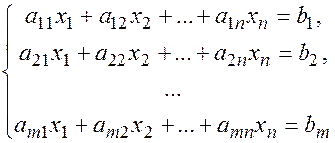(14.1)

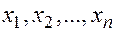называют системой m линейных алгебраических уравнений с неизвестными . Коэффициенты 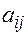называются коэффициентами системы и записываются в виде матрицы:

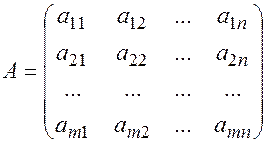(14.2)

числа, стоящие в правых частях уравнений (14.1), образуют матрицу вектор– столбец

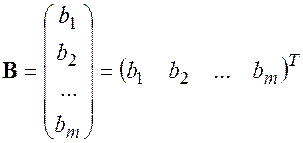(14.3)

называемую столбцом свободных членов.

Матрица системы, дополненная столбцом свободных членов, называется расширенной матрицей системы и обозначается (в данной главе)

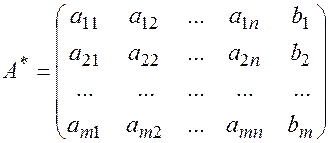(14.4)

Если все свободные члены системы тождественно равны нулю, то система называется однородной, в противном случае – неоднородной.

Определение.Решением СЛАУ называется такая совокупность -чисел 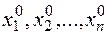которая при подстановке в систему вместо 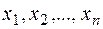обращает все уравнения системы в тождества.

Прежде чем переходит к решению системы, запишем её в матричном виде. Мы уже вводили матрицу коэффициентов 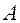и матрицу – столбец свободных членов 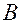, введем матрицу – столбец неизвестных

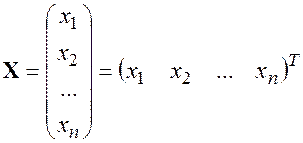(14.5)

Найдем произведение матрицы 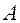на столбец неизвестных :

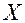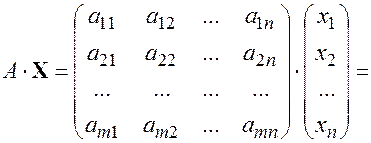
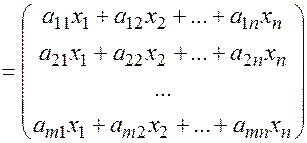
по правилу умножения матриц данное произведение представляет собой столбец, состоящий из 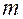элементов, которые равны соответствующим левым частям уравнений системы 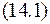. Из определения равенства двух столбцов следует, что система 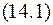равносильна одному равенству между столбцам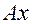и и 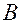. Таким образом, в матричной записи система 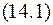равносильна равенству .

Системы называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной если она имеет по крайней мере два различных решения. Приведем пример неопределенной системы.

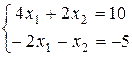
Данная система является совместной и неопределенной, поскольку у нее имеется, по крайней мере, два различных решения:

1) ;

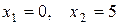2) .

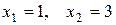СЛАУ называется однородной, если правые части всех уравнений равны нулю, то есть :

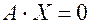
Если в СЛАУ хотя бы один из свободных членов отличен от нуля: 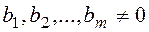, то система называется неоднородной.

Система называется квадратной, если число уравнений равно числу неизвестных: .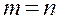

Определение.Решением СЛАУ называется такая совокупность -чисел 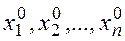которая при подстановке в систему вместо неизвестных 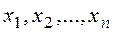обращает все уравнения системы в тождества.

СЛАУ называется совместной, если она имеет хотя бы одно решение.

СЛАУ называется несовместной, если у нее не существует ни одного решения.

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора, или число линейно независимых строк (столбцов) матрицы. Обозначается .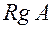

Теорема. (Кронекера-Капелли)Для того чтобы СЛАУ являлась совместной (т.е. имела решение) необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу основной матрицы системы, т. е. 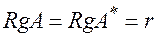. Причем:

1) если 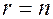система имеет единственное решение;

2) если 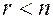система имеет бесконечное множество решений зависящих от 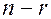свободных неизвестных.

Следствие. Если 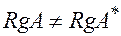, то система несовместна (нет решений).

Решение СЛАУ размерности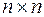

1) Метод Крамера.

Рассмотрим систему из двух уравнений с двумя неизвестными:

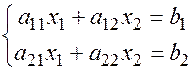
Выразим в системе переменную 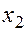избавившись от переменной .

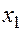Поделим первое уравнение на элемент 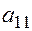и умножим полученный результат на .

,

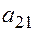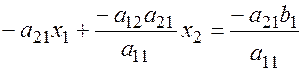Складываем со вторым уравнением системы и выражаем переменную .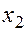

.

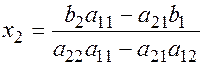В полученной дроби в числителе стоит определитель 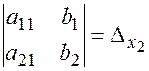, а в знаменателе основной определитель системы .

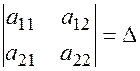И мы получили формулу 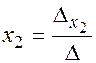. Аналогичными вычислениями мы получим 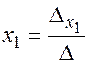, где .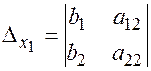

Рассмотрим правило Крамера для системы уравнений 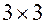, наложив условие линейной независимости уравнений системы.

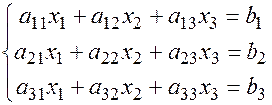
Кроме основного определителя системы введем в рассмотрение дополнительные определители, получаемые заменой коэффициентов 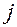-го столбца столбцом свободных членов.

, ,

.

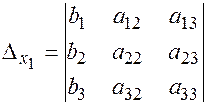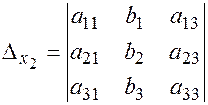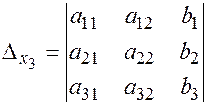Умножим каждое уравнение системы на алгебраические дополнения первого столбца и сложим левые и правые части полученных равенств:

.

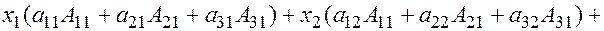
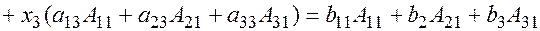Используя следствие 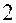свойства 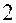определителей получаем:

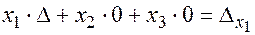или .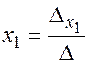

Поступая аналогичным образом получим следующие формулы Крамера для определения неизвестных системы:

, , .

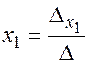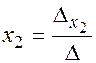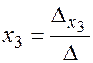Теорема (формулы Крамера): Система из n уравнений с n неизвестными

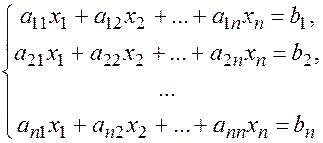
в случае, когда определитель системы отличен от нуля , имеет единственное решение определяемое формулами:

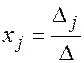(14.6)

(для всех 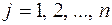), где через обозначен определитель основной матрицы системы, а 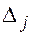- дополнительные определители, получаемые из Δ заменой 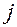-го столбца столбцом свободных членов, т.е.

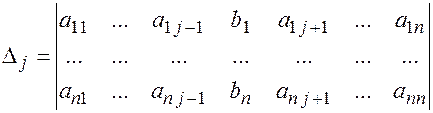(14.7)

2) Метод Гаусса.

Метод Гаусса относится к наиболее эффективным методам решения СЛАУ. Этим методом решаются как квадратные, так и прямоугольные системы линейных уравнений. В основе метода Гаусса лежат прямой и обратный ход. Прямым ходом расширенную матрицу системы элементарными преобразованиями сводят к треугольному виду. Обратным ходом находят неизвестные величины.

К элементарным преобразованиям относится:

1. Перестановка двух любых уравнений системы;

2. Умножение любого уравнения системы на произвольное, отличное от нуля, число;

3. Прибавление к произвольному уравнению системы любого другого уравнения, умноженного на произвольное число.

Методом Гаусса можно решать и прямоугольные системы.