Евклидово пространство. Введенные нами линейные пространства существенно отличаются от множества векторов обычного геометрического тем
Введенные нами линейные пространства существенно отличаются от множества векторов обычного геометрического тем, что в линейном пространстве не определены понятия длины вектора и угла между ними.
Введем понятия длины и угла с помощью скалярного произведения.
Определение. Вещественное линейное пространство называется евклидовым, если в нем определена операция скалярного произведения: любым двум векторам 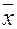 ,
, 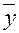 сопоставлено вещественное число обозначаемое
сопоставлено вещественное число обозначаемое 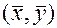 и удолетворяет условиям:
и удолетворяет условиям:
1) 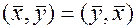 ;
;
2) 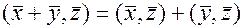 ;
;
3) 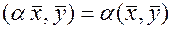 ;
;
4) 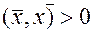 , если
, если  .
.
Следствием из этих аксиом являются:
1) 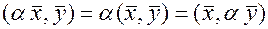 ,
, 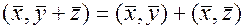 ;
;
2) Последовательно применяя аксиомы 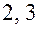 легко доказать, что для любых векторов и чисел
легко доказать, что для любых векторов и чисел
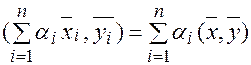 ;
; 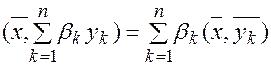 .
.
3) Каков бы ни был вектор 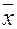 , имеем
, имеем 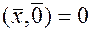 . Действительно, положим Назовем длиной вектора
. Действительно, положим Назовем длиной вектора 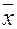 и обозначим
и обозначим 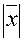 число
число 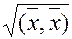
Углом между векторами 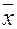 ,
, 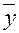 назовем каждое число
назовем каждое число 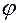 , удовлетворяющее условию:
, удовлетворяющее условию: 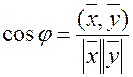 .
.
В силу аксиомы 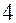 длина вектора вещественное неотрицательное число.
длина вектора вещественное неотрицательное число.
С определением величины угла дело обстоит сложнее. Нам предстоит доказать, что выражение в правой части равенства не превосходит единицы т.к. максимальное значение 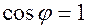 , то
, то 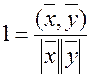 отсюда
отсюда 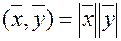 .
.
Если известно, что 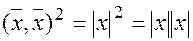 , тогда
, тогда 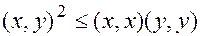 - неравенство Коши-Буняковсного.
- неравенство Коши-Буняковсного.
Пусть 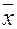 ,
, 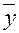 - любые векторы принадлежащие
- любые векторы принадлежащие 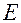 . Для любых
. Для любых 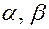 имеем
имеем
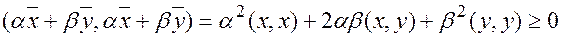 . Положим
. Положим 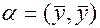 ,
, 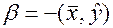 , то получим
, то получим 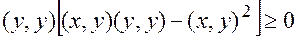 , откуда и вытекает требуемое неравенство треугольника
, откуда и вытекает требуемое неравенство треугольника 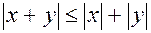
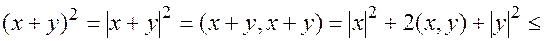
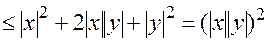 .
.
Векторы будем называть ортогональными, если 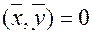 для любых
для любых 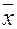 ,
, 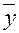 .
.
Дата добавления: 2015-08-26; просмотров: 714;
