Примеры конкретных линейных пространств.

1. – -мерное координатное пространство или совокупность строк содержащих – вещественных чисел. Операция сложения и умножения на число определены следующим образом:

а) ;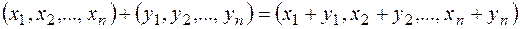

б) .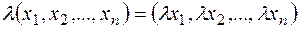

Аксиомы 1-8 проверяются элементарно.

2.Множество 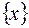всех положительных вещественных чисел. Под суммой [x+y]=x*y (будем понимать произведение), а под умножением [λ*x]=x^λ, тогда нулевым элементом множества будет являться 1, а противоположным x, 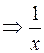, тогда аксиомы 1-8 легко проверяются.

3.Множество всех положительных вещественных чисел 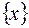, где сумма и умножение на число определяются стандартным образом [x+y]=x+y, [λx]= λx не является линейным пространством.

4.Аналогично множество всех многочленов степени 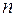не является линейным пространством, т. к. сумма может оказаться степени < .

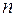Определение. Линейной комбинацией элементов 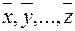пространства 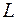называются выражения вида 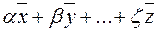, где 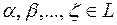, говорят что 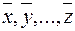- линейно зависимы, если 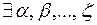, такие что 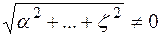, а .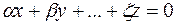

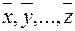- неявляющиеся линейно зависимыми называют линейно независимыми.

Определение.Совокупность линейно независимых элементов 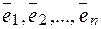пространства 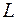называется базисом этого пространства, если для 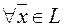существуют 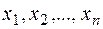(вещественные числа), такие, что справедливо равенство 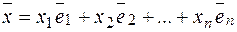, где 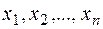- координаты (коэффициенты) 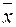в базисе 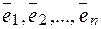пространства .

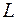Теорема.При сложении любых двух элементов линейного пространства 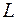их координаты (относительно любого базиса) складываются; при умножении произвольного элемента на любые числа α все координаты этого элемента умножаются на α.

Доказательство. Пусть базис ,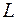

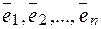
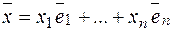и 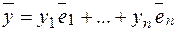- два элемента .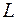

Тогда в силу аксиом 1-8 ,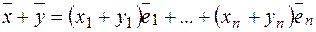

.

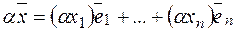Определение.Линейное пространство 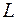называется n-мерным, если в нем существует n-линейно независимых элементов, а любые ( 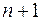) элементы уже являются линейно зависимыми, 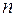– называют размерностью 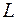и обозначают 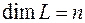. Линейное пространство 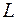называют бесконечномерным, если в нем существует любое число линейно независимых элементов.

Теорема. Если 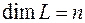, то любые 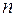- линейно независимых элементов этого пространства образуют базис.

Если линейное пространство 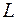имеет базис, состоящий из 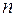элементов, следовательно, .

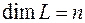Определение (понятие линейного подпространства). Подмножество 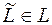и удовлетворяющее условиям:

1. если 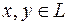, то ;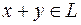

2. если ;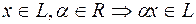

называется линейным подпространством (или просто подпространством) пространства R.

Определение. Линейной оболочкой 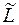элементов 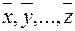называется совокупность всех линейных комбинаций этих элементов, т. е. множество элементов вида 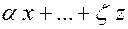, где 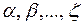(любые действительные числа), линейную оболочку принято обозначать как 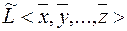, ясно, что 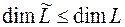. 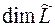равна максимальному числу линейно независимых элементов 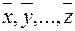(которые составляют базис линейной оболочки).

Определение (новое определение ранга матрицы). Ранг произвольной матрицы 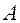равен максимальному числу линейно независимых строк (или столбцов) этой матрицы.