Ортонормированный базис.
Определение.Систему векторов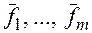 
в евклидовом пространстве назовем ортонормированной, если 
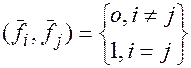каковы бы ни были номера 
.
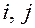Утверждение. Ортонормированная система векторов линейно независима.
Док-во. Пусть нам дана ортонормированная система векторов. Рассмотрим ее линейную комбинацию: 
. Из которой вытекает, что 
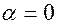при произвольном 
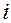. В самом деле умножим обе части равенства скалярно на 
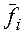. Все слагаемые, кроме 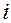-го обратятся в 
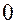, и мы получим 
.
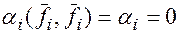Т.о. каждая равная нулю линейная комбинация векторов 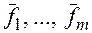необходимо тривиальна.
В 
-мерном евклидовом пространстве существует ортонормированная система из векторов, и эта система является ортонормированным базисом.
Процесс ортогонализации линейно независимых элементов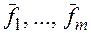 
выглядит следующим образом:
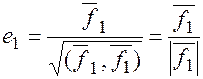
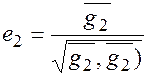,где 
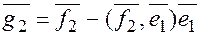
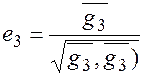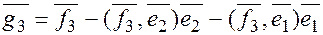
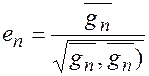,где 
где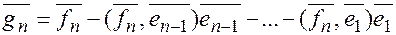 
.
Дата добавления: 2015-08-26; просмотров: 969;