Линейная независимость векторов. Базис. Размерность линейного пространства
| Def.1 | Векторы 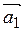 , , 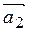 , …, , …, 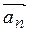 называют линейно независимыми, если равенство называют линейно независимыми, если равенство 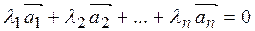 выполняется тогда и только тогда, когда все числа равны нулю, т.е. выполняется тогда и только тогда, когда все числа равны нулю, т.е. 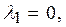 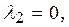 …, …, 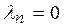 . В противном случае они называются линейно зависимыми. . В противном случае они называются линейно зависимыми.
|
Пусть, например, 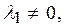 тогда вектор
тогда вектор 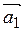 можно представить в виде линейно комбинации остальных векторов, т.е.
можно представить в виде линейно комбинации остальных векторов, т.е.
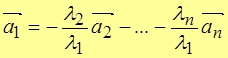 .
.
| Def.2 | Размерностью линейного пространства L называют максимальное число линейно независимых векторов данного пространства и обозначают 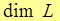 . .
|
| Def.3 | Базисом данного пространства L называют совокупность линейно независимых векторов пространства L, число которых равно размерности пространства L. |
Дата добавления: 2015-08-20; просмотров: 812;
